- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Golden Math
Unlike Euclidean and more recent geometries, ancient geometry rests on no a priori axioms. The start point of ancient geometric thought is not a set of intellectual or abstract definitions, but a meditation upon the methaphysical Unity. Ancient Geometry begins with One, whereas modern geometry begins with Zero.
We could define Golden Math, or Sacred Math, as the mathematics that naturally arise from the study of Unity.
Roman numerals use a notation similar to that of Egyptian numeration. Both were based on groupings that did not require a zero to indicate an empty column. For example, in roman 1505=MDV. The ancient Egyptian numerical progression began with one rather than zero:
Geometry hides in plain sight many complex mathematical relationships. The circle is perhaps the most natural representation of Unity. Sometimes it is presented with a dot in the middle (the symbol of the Monad) which refers to the Tao, the essence of all Creation.
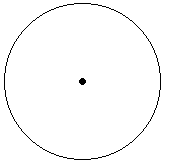
Although not readily apparent, this simple figure hides within the essence of recurrence. You can plug into the inner circle and draw a central point, and this operation can be repeated indefinitely. Many other non circular geometric figures show this principle more visibly (think of the square, the hexagon, etc.), but the circle also contains it. Obviously, the circle also shows recurrence in the outer direction. Recurrence is one of the principles of creation that we see everywhere in Nature, like in the growth of plants.
If you take the radius of the circle to be One, then you discover that the circle hides another key number in its perimeter, the generative number π.

This is a symbol of periodicity, of cyclicity. Everything in our life works in cycles: birth and death, night and day, an hour; even when you go shopping you are doing a cycle: you enter the shop, pick whatever you need, and pay; and you probably repeat this cycle many times a week without even noticing that it is a cycle!
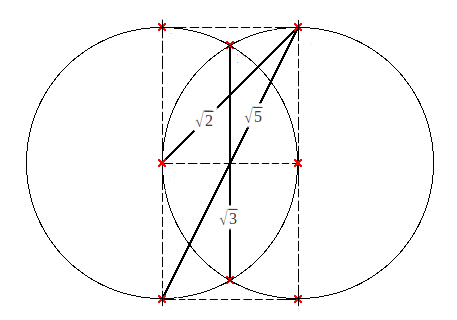
When you draw two circles, multiplicity arises, as when you draw a square. The symbol of the Vesica Piscis, two circles interleaced, although not being squared, also hides another set of basic generative numbers, which are the square roots of 2, 3 and 5:
The last generative number that we must introduce, which is perhaps the more important one, is the Golden Ratio φ. It provides the only way of dividing a unit segment into two peaces, using a single number and its square, which are in geometric proportion:
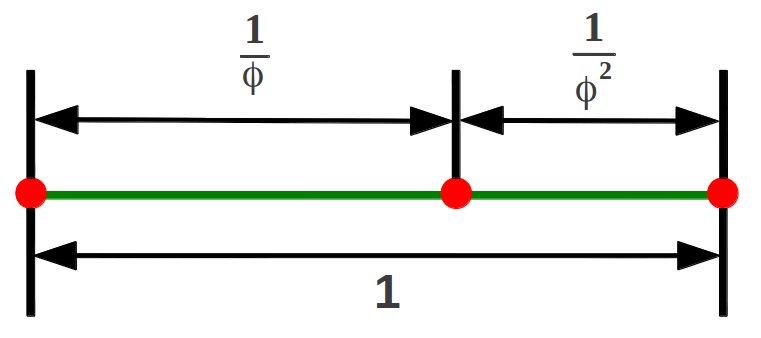
And this division can be iterated indefinitely with the same proportion for any of the splitted segments. In fact, the continued fraction representation of φ already shows that the Golden Ratio also hides the recursivity whithin:
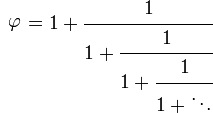
I wouldn't like to finish this introduction without mentioning a sequence that is central in Golden Math, and also closely related to the Golden Ratio: the Fibonacci sequence:
As you may know, this sequence also arises everywhere in Nature. In fact, Nature uses to approximate the Golden Ratio in the growth of most life forms. This is readily apparent in plants. If you count the number of petals in most flowers, you will notice that almost always it is a Fibonacci number (in the pictures below, 13 and 21 petals). And when it is not, as explained here, it uses to be a number from Lucas sequence, another important sequence that we will talk about in our section on the Golden Ratio. Perhaps less known is the fact that in some plants the number of branches at any stage of developement is a Fibonacci number, as is also the number of leaves in any stage (see figure below reproduced from here).



