- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Phi in Sacred Solids
1.- Introduction
The Platonic solids can be classified into two groups: those without the Golden Ratio in their constitution (the tetrahedron, the cube and the octahedron) and those which do involve the Golden Ratio, namely the Dodecahedron and the Icosahedron. These two groups are invariant under the dual operation, i.e. the duals of all these solids remain in the same group. Something similar happens in the Archimedean and their duals the Catalan solids: for example the cuboctahedron and its dual, the rhombic dodecahedron, pertain to the first group (non Golden Ratio related).
In every discussion about Metatron's Cube one finds the assertion that this structure contains all the Platonic solids inside it. In my article on Metatron's Cube I have shown that this is not true: the inner grid of the cube is a tesselation of space composed of tetrahedrons and octahedrons alternated. The solids that can be found in Metatron's Cube do not involve the Golden Ratio: its inner grid generates the tetrahedron, the octahedron, the star tetrahedron, and the cuboctahedron, but neither the icosahedron nor the dodecahedron. This fact may induce a side question: do these two Golden Ratio related solids form any grid? Perhaps. What I will show is that the inner interconnection of their vertices and the outer prolongation of their edges lead to a set of interconnected Stellations, such as the one known elsewhere as the Double Pentadodecahedron.
I have not been able to find any convex polyhedron that contains all five Platonic solids, namely whose vertices in cartesian coordinates allow the construction of them all. The closest approximation to this task is the Rhombic Triacontahedron: I will show that its vertices define all the Platonic solids except the octahedron. If one whishes to include the vertices of the octahedron, one is led to an amazing non-convex polyhedron which does truly contain all the Platonic solids, and much more: it is known as the 120 Polyhedron, and has bee extensively studied by Robert W. Ray.
2.- The Golden Ratio in Platonic Solids
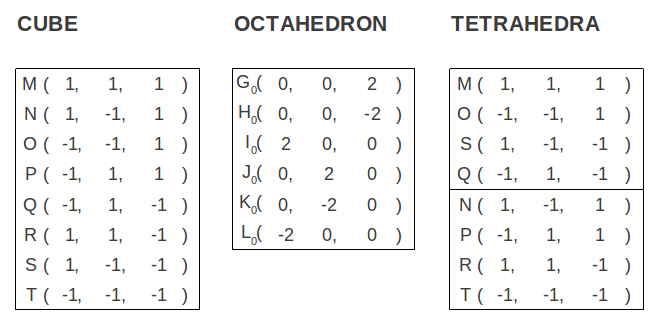
It is well known that the simplest regular polyhedron, the tetrahedron, is contained inside the cube. Therefore it can be constructed with half the vertices of a cube (Figure 1). The dual of the later is the octahedron, so its vertices are the midpoints of the faces of the cube. All these solids have in common the fact that their cartesian coordinates do not involve the Golden Ratio. In fact, all of them can be defined by points in space with integer coordinates (see Figure 1 and Table 1).
 |
 |
 |
 |
| (a) | (b) | (c) | (d) |
| Figure 1: The octahedron, the cube and the two tetrahedra contained whithin the latter, which define a star tetrahedron or stellated octahedron. | |||
 |
||
| Table 1: The vertices of the cube, octahedron and tetrahedron shown in Figure 1, in cartesian coordinates. All of them can be derived using integer numbers. |
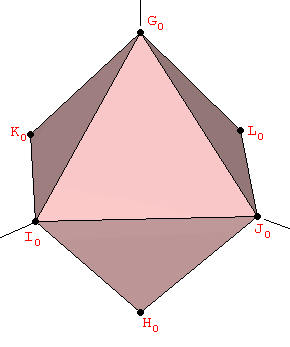
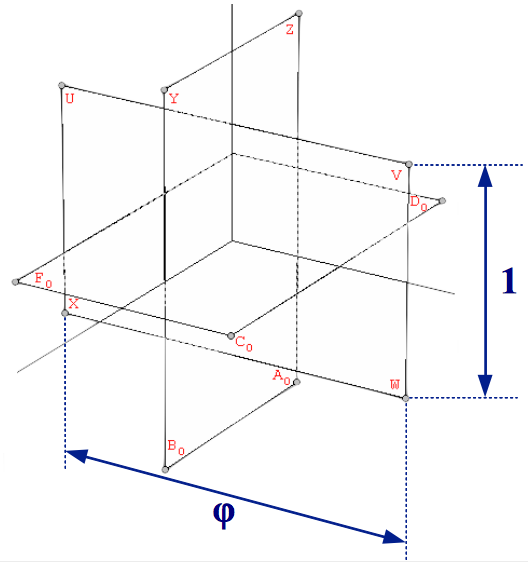
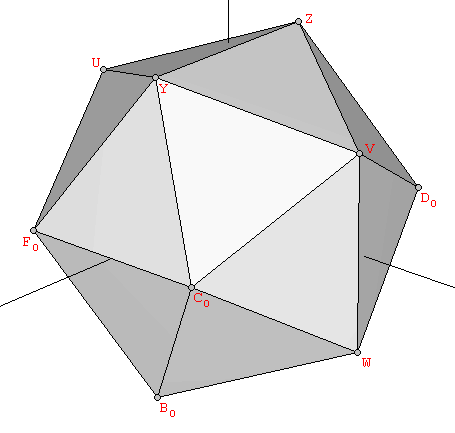
On the other hand, for constructing the solids in the second group, their vertices in cartesian coordinates must contain the Golden Ratio. The vertices of the Icosahedron can be easily obtained from three mutually orthogonal Golden rectangles, whose sides are in a proportion 1:φ (the actual edge length of all the polyhedra shown in the figures of this article is twice the one shown by the blue arrows that indicate the Golden proportions). The edges of the icosahedron are the segments that join each of the rectangle's vertices with their five nearest neighbours, as shown in Figure 2 (if, instead, one joined each vertex with the five opposite vertices to those five nearest ones, one would obtain a nice stellation of the dodecahedron known as the small stelladetd dodecahedron, see Section 3):
 |
 |
|
| (a) | (b) | |
| Figure 2: The vertices of the icosahedron are defined by three mutually orthogonal Golden rectangles. | ||
 |
||
| Table 2: The vertices of the icosahedron in cartesian coordinates. |
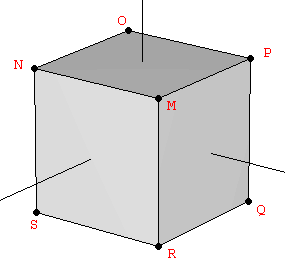
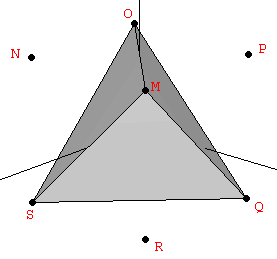
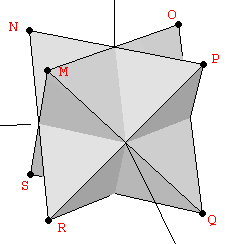
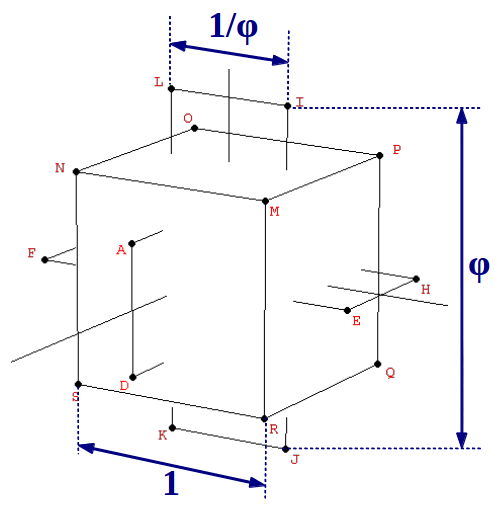
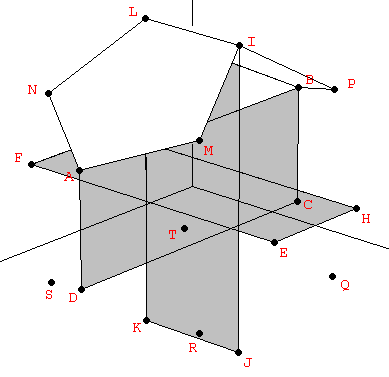
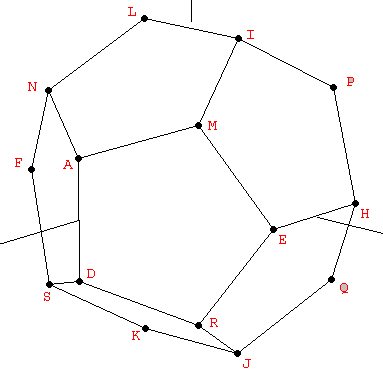
For constructing the dodecahedron, it is helpful to know that the cube is contained in its interior. Starting with the eight vertices of a cube, the remaining twelve vertices can be obtained from three orthogonal rectangles also related to the Golden Ratio, but in a proportion 1:φ2 instead of 1:φ as in the icosahedron (Figure 3):
 |
 |
 |
| (a) | (b) | (c) |
| Figure 3: The vertices of the dodecahedron can be obtained from the cube and three mutually orthogonal Golden rectangles with a side relationship 1:φ2. | ||
 |
||
| Table 3: The vertices of the dodecahedron shown in Figure 3, in cartesian coordinates. |
3.- The Golden Ratio in Stellations
3.1.- The Golden Ratio in the Small Stellated Dodecahedron
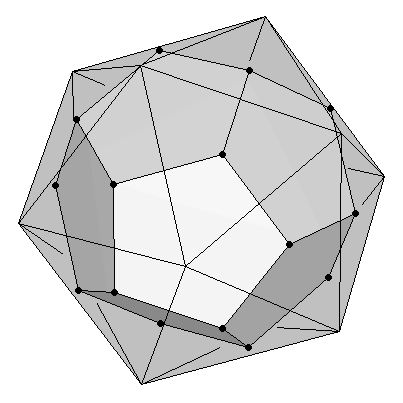
The dodecahedron and the icosahedron are duals of each other. That means that, starting from an icosahedron, a dodecahedron can be easily obtained by joining the midpoints of the icosahedron's faces (Figure 4a). And conversely, an icosahedron is formed by joining the midpoints of the faces of a dodecahedron (Figure 4b).
 |
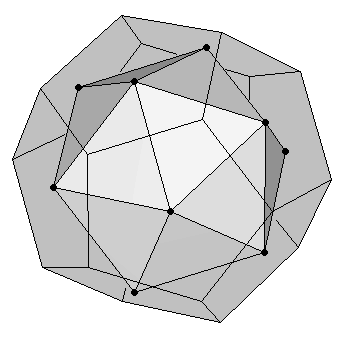 |
| (a) Dodecahedron as dual of an icosahedron | (b) Icosahedron as dual of a dodecahedron |
| Figure 4 | |
In fact, if one traces twelve lines starting from the center of the dodecahedron and crossing the midpoints of its faces, any set of twelve points located on these lines and equidistant from the central point will also define an icosahedron, although at a different scale. A very interesting particular case of these infinite set of icosahedrons is the one obtained as follows: take a dodecahedron and extend its edges untill they meet again at some distant points. You will find that every set of five extended edges converges at a point located on the twelve lines mentioned above; therefore they are the vertices of an icosahedron. They can also be obtained by symmetrically extending the short sides of the rectangles that compose the dodecahedron until a Golden rectangle is reached (Figure 5)..
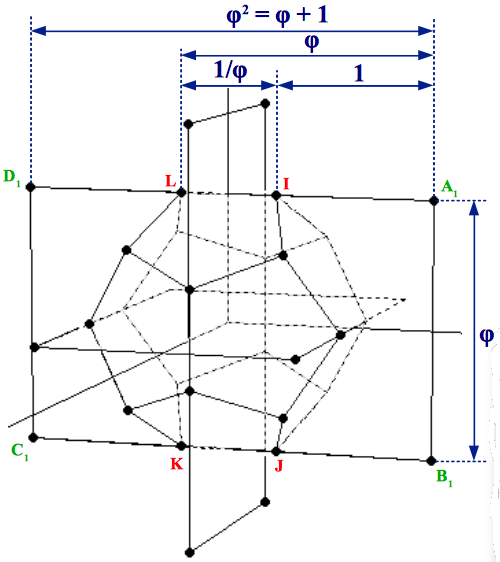 |
||
| Figure 5: Extending the three 1:φ Golden rectangles of a dodecahedron until three 1:φ2 Golden rectangles are obtained provides the vertices of a special icosahedron: the one that gives rise to the Small Stellated Dodecahedron. |
There are two interesting facts about this special icosahedron: the first one is that it has an edge size in a proportion 1:φ2 with the edge size of the original dodecahedron, which can be clearly appreciated in the preceding figure. But the other fact is that the process of extending the edges of the dodecahedron ends in a nice stellation known as the Small Stellated Dodecahedron (Figure 6).
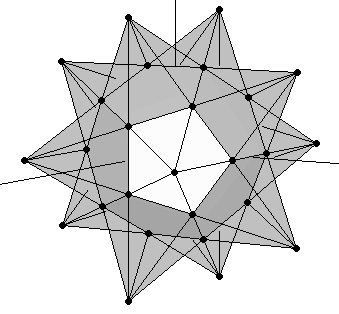 |
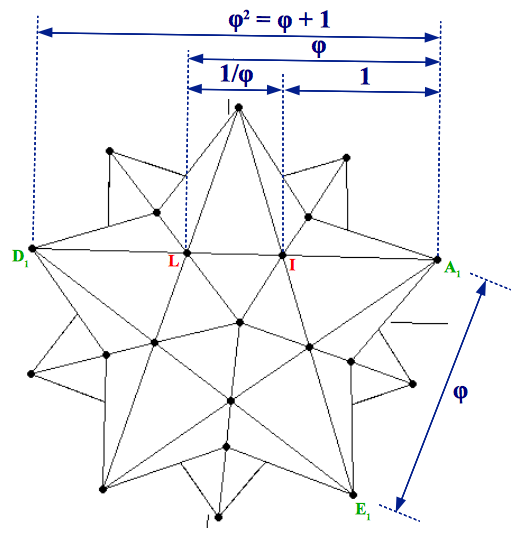 |
| (a) | (b) |
| Figure 6: The small stellated dodecahedron contains three powers of the Golden Ratio. This can be clearly appreciated in its pentagram faces. Its outer vertices define an icosahedron whose edge length (A1E1) is in a proportion 1:φ2 with the edge of the original dodecahedron (IL). | |
 |
||
| Table 4: The cartesian coordinates of the small stellated dodecahedron. The vertices of the original dodecahedron (Table 3), though visible, are not vertices of the stellation. |
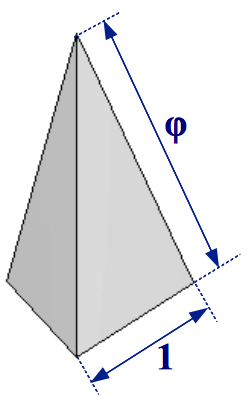
This amazing nonconvex polyhedron contains three powers of the Golden Ratio inside it (Figure 6b). If the edge length of the original dodecahedron is taken as unity, the small stellated dodecahedron can be seen as an extension of this dodecahedron by placing a five-sided Golden pyramid on top of each of its faces. A Golden Pyramid has an apotem in a proportion 1:φ with its base side, therefore each of its lateral faces are Golden gnomons (Figure 7).
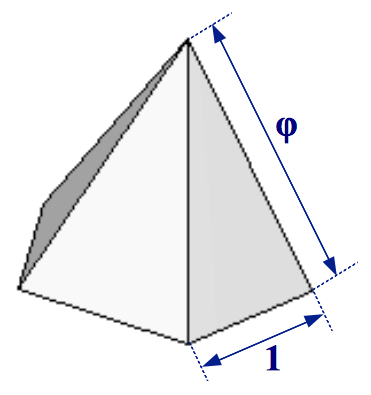 |
 |
|
| (a) Pentagonal Golden pyramid | (b) Triangular Golden pyramid | |
| Figure 7 | ||
3.2.- The Golden Ratio in the Great Stellated Dodecahedron
As it happens with its counterpart the small stellated dodecahedron, there are several ways to study the construction of the great stellated dodecahedron. As a stellation, it is the result of extending the vertices of a regular icosahedron until they meet in a new set of points. How many points? Easy to guess: if the stellation of a dodecahedron led to the 12 vertices of an icosahedron, the stellation of the icosahedron will lead to the 20 vertices of a dodecahedron. Let's see in what proportion.
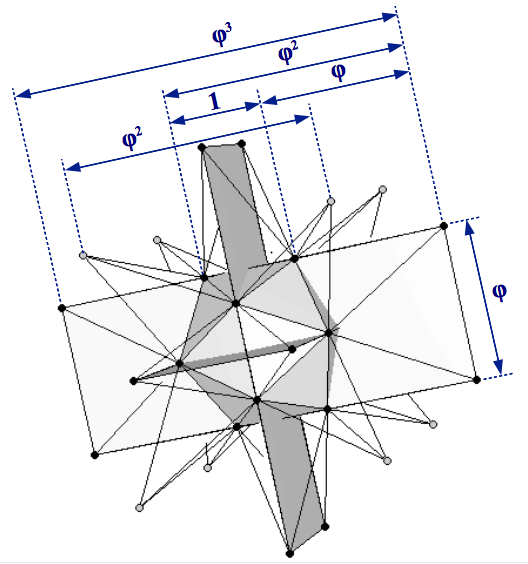 |
 |
| (a) | (b) |
| Figure 8: (a) Construction of the great stellated dodecahedron starting from an icosahedron of unit edge length. The outermost black bullets describe the 1:φ2 rectangles of a dodecahedron, whereas the grey bullets are the vertices of a cube. (b) The Golden Ratio proportions can be clearly appreciated in the pentagram faces. | |
The process can be divided into two steps. The first step is to symmetrically extend the three 1×φ Golden rectangles of the original icosahedron until they form the three 1:φ2 rectangles necessary for a dodecahedron (Figure 8a). Taking the edge size of the icosahedron as unity, the actual size of these extended rectangles will be φ×φ3. This is more clearly appreciated when observing the pentagram faces of the great stellated dodecahedron (Figure 8b). These rectangles only provide twelve of the twenty vertices of a dodecahedron. As we have seen in section 2, the remaining eight vertices form a cube. Following the proportions shown in Figure 3 and Table 3, this cube must have an edge size of φ2 (Figure 8a).
The construction of the great stellated dodecahedron can also be thought of as starting from the icosahedron and putting a triangular Golden pyramid (Figure 7b) on top of each of its twenty faces. The resulting stellated polyhedron is shown in Figure 9.
 |
 |
| (a) | (b) |
| Figure 9: The great stellated dodecahedron and its inner icosahedron. | |
 |
||
| Table 5: The cartesian coordinates of the great stellated dodecahedron. The vertices of the original icosahedron (Table 2), though visible, are not vertices of the stellation. |
3.3.- The Double Pentadodecahedron
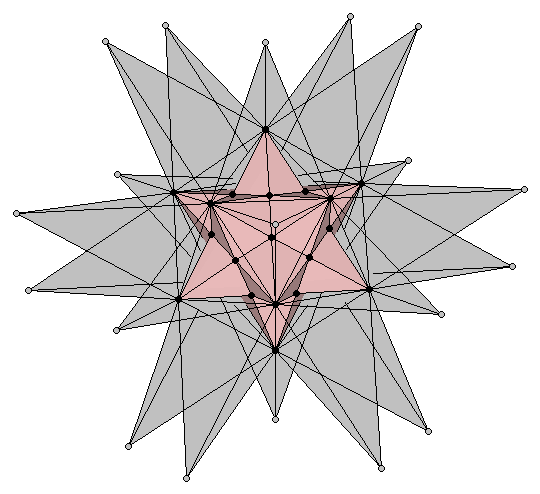
The procedure outlined in the two preceding sections can also be followed in sequential order: Starting with a dodecahedron, extend its edges to form a small stellated dodecahedron. As the later's vertices describe an icosahedron, its (imaginary) edges can be further extended until obtaining a great stellated dodecahedron (Figure 10a). The result of the whole process is a great stellated dodecahedron that contains a small stellated dodecahedron whithin (Figure 10b).
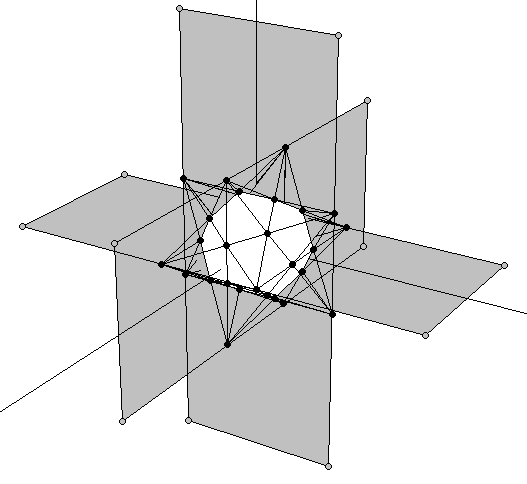 |
 |
| (a) | (b) |
| Figure 10: (a) Extension of the Golden rectangles of the small stellated dodecahedron to form the 1:φ2 rectangles of an external dodecahedron that describes the vertices of the Double Pentadodecahedron (grey bullets). As described in section 3.2 (Figure 8) it only remains adding the vertices of a final cube in the right proportion. (b) A semitransparent view of the double pentadodecahedron that shows its inner small stellated dodecahedron. | |
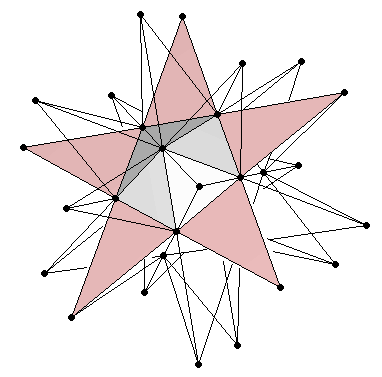
This polyhedron is known as the Double Pentadodecahedron. Its name stems from the fact that each of the twelve inner points of the great stellated dodecahedron -which coincide with the vertices of the small stellated dodecahedron cointained whithin- has two pentagrams associated with it (the pink and the blue ones shown in Figure 11). It is remarkable the fact that the double pentadodecahedron contains five powers of the Golden Ratio (Figure 11).
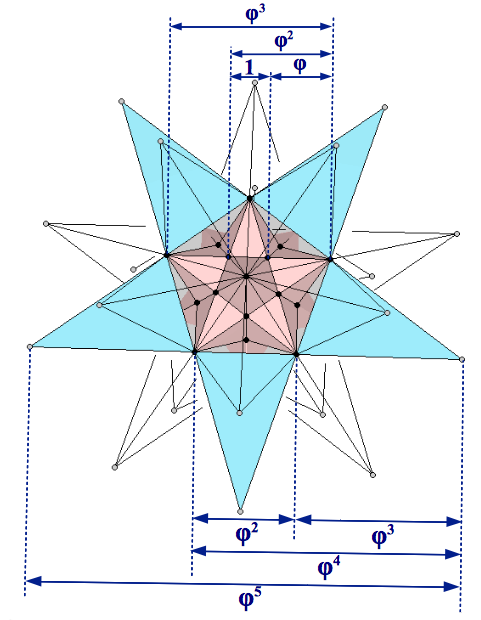 |
| Figure 11: The double pentadodecahedron has an inner small stellated dodecahedron, each of whose 12 vertices has 2 associated pentagrams (highlighted in pink and blue in the figure). Notice that this double stellation contains 5 powers of the Golden Ratio. |
Several authors hold that the double pentadodecahedron describes the new energetic cristalline grid that is being activated on planet Earth at the current time. This grid is supposed to allow us an easier access to the non-physical dimensions that exist above our physical reality in three dimensions.
4.- The Golden Ratio and the Rhombic Triacontahedron
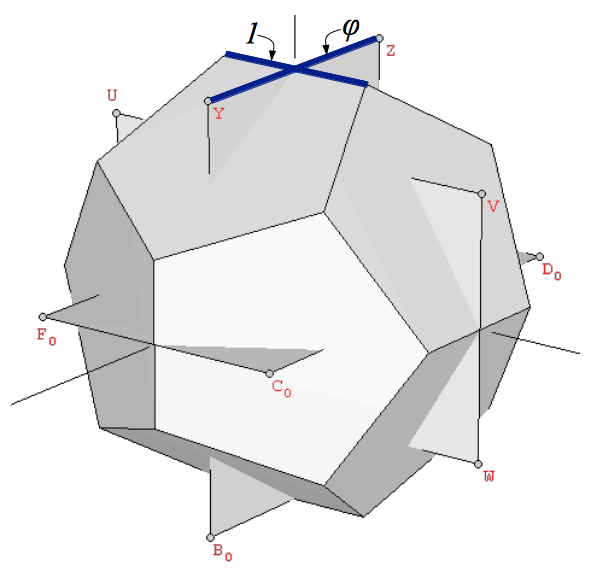
What's the result of putting together the vertices of a dodecahedron and an icosahedron, both at the same scale? It depends on their relative orientation. We say that a dodecahedron and an icosahedron are at the same scale when the larger side of their constituent Golden rectangles (of proportions 1:φ2 and 1:φ) has the same length. Two individual polyhedra that meet this first requirement can be oriented in many different ways relative to one another. The key orientation is the one in which the three Golden rectangles of the icosahedron and the dodecahedron are exactly orthogonal to one another, and have their larger sides parallel (Figure 12).
 |
 |
| (a) | (b) |
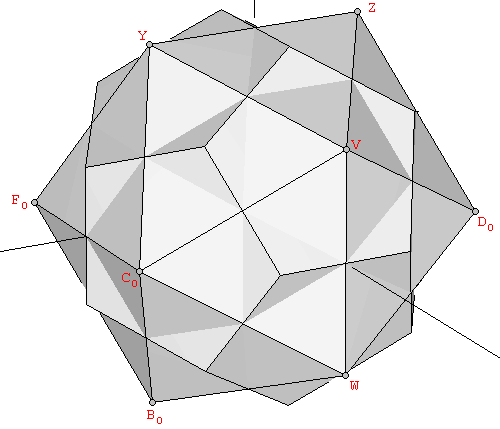
| Figure 12: (a) We say that an icosahedron and a dodecahedron are at the same scale when the larger side (vertical in the figure) of their constituent Golden rectangles has the same length. (b) The polyhedra resulting from the superimposition of a dodecahedron and an icosahedron at the same scale. We can see that the 30 edges of both polyhedra are orthogonal to each other and define the diagonals of 30 Golden rhombi. | |
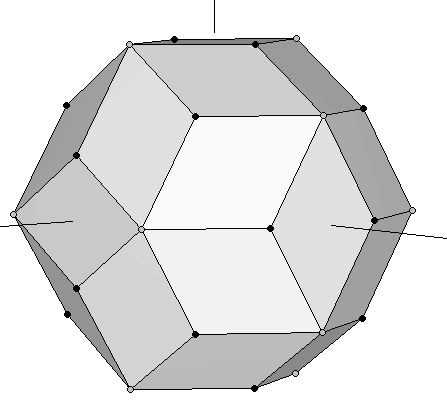
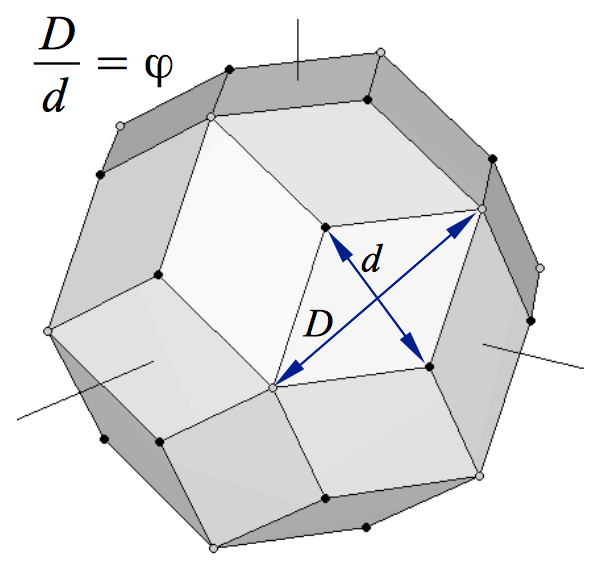
The two preceding requirements happen to be exactly met by the dodecahedron and the icosahedron shown in Figures 2 and 3, whose coordinates are collected in Tables 2 and 3. In this case the coinciding larger side of the Golden rectangles has a common length of 2φ. If we superimpose the two polyhedra, we obtain a nonconvex polyhedron (Figure 12b). We can observe this figure that the shorter sides of each couple of mutually orthogonal dodecahedron-icosahedron Golden rectangles are in a Golden Ratio (in this case, their lengths are 2/φ and 2). They constitute the two diagonals of a Golden Rhombus. In fact, Figure 12b shows that all the coplanar edges of our dodecahedron and icosahedron intersect orthogonally defining 30 Golden Rhombi. Finally, if we form the convex polyhedron that joins all their vertices, the result is a Rhombic Triacontahedron (Figure 13).
 |
 |
| (a) | (b) |
| Figure 13: Rhombic Triacontahedron formed by joining a dodecahedron and an icosahedron at the same scale. The vertices of the original dodecahedron are the black bullets, whereas the grey ones are the vertices of the icosahedron. | |
With our construction process, we have established that the 30 faces of a rhombic triacontahedron are Golden rhombi whose shorter and longer diagonals define the edges of a dodecahedron and an icosahedron, respectively. The rhombic triacontahedron is a semiregular polyhedron whose vertices define almost all the Platonic Solids, because the cube is contained inside the dodecahedron, and the tetrahedron is contained inside the cube (Figures 1 & 3). Although some authors claim that it also contains the octahedron, it is not stritly true. To make it "appear" we would need to add the central points of the faces of the cube, which are not vertices of the rhombic triacontahedron. The following polyhedron solves this problem.
5.- The 120 polyhedron
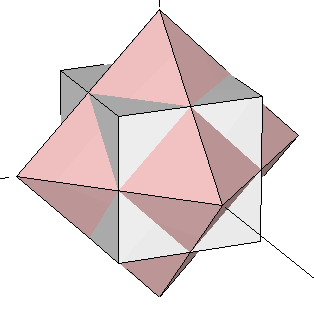
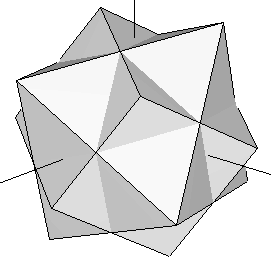
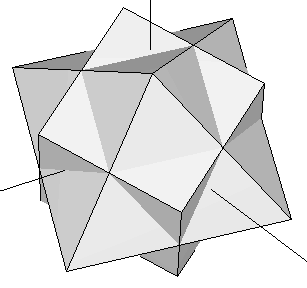
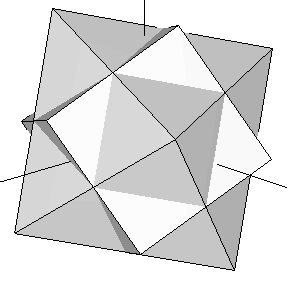
Let's take the cube contained in our original dodecahedron (Figure 3) and join it with an octahedron whose edges intersect the cube's at their exact midpoints (i.e. we join the cube of Figure 1b with the octahedron of Figure 1a). Now rotate the complex until the cube matches another set of eigth vertices in the dodecahedron that contains it. This process can be done in four different ways. The resulting set of vertices of the five rotated cubes define the dodecahedron (some of these vertices are repeated). If we add, at the same scale, our icosahedron to this dodecahedron, we obtain the rhombic triacontahedron studied in the preceding section (Figure 13). The set of 30 vertices of our five rotated octahedra happen to fall on top of each of the Golden Rhombi of that rhombic triacontahedron. Their coordinates are shown in Table 6 below.
 |
 |
 |
 |
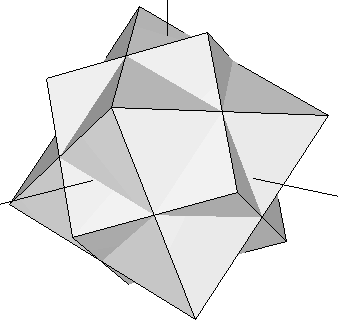 |
| Figure 14: Superimposition of the octahedron and the cube of Figure 1. At each step in this process, the complex is rotated so that the cube moves to a new set of eight vertices of the dodecahedron that contains it. The octahedron rotates accordingly, defining a set of 6 new vertices at each step (see Table 6). | ||||
 |
||
| Table 6: The cartesian coordinates of the five rotated octahedra shown in Figure 14. |
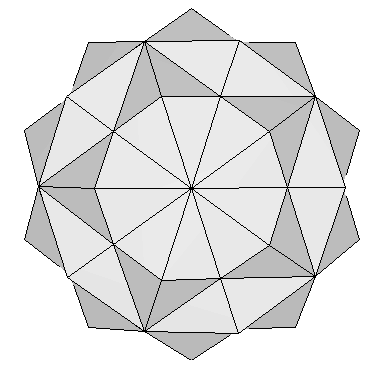
Putting together the 20 vertices of the dodecahedron and the 12 vertices of the icosahedron, we have the 32 vertices of the rhombic triacontahedron (Figure 12 & 13). Now we add to this set the 30 vertices of the preceding octahedra. The final result is a set of 62 vertices that defines a beautiful nonconvex polyhedron known as the 120 polyhedron (Figure 15):
 |
 |
 |
| (a) | (b) | (c) |
| Figure 15: Three different views of the 120 polyhedron. It contains the vertices of the dodecahedron, the icosahedron, and the five rotated octahedra. | ||
This polyhedron has been extensively studied by Robert W. Ray. It has 120 faces, because each of the 30 faces of the rhombic triacontahedron has been "augmented" by a small four-sided pyramid. Those 30 pyramids have very special dimensions. Not only their base is a Golden rhombus, but their base size and their shortest apothem are also in Golden Ratio. This can be easily shown from the coordinates provided in Tables 2, 3 and 6 as follows:
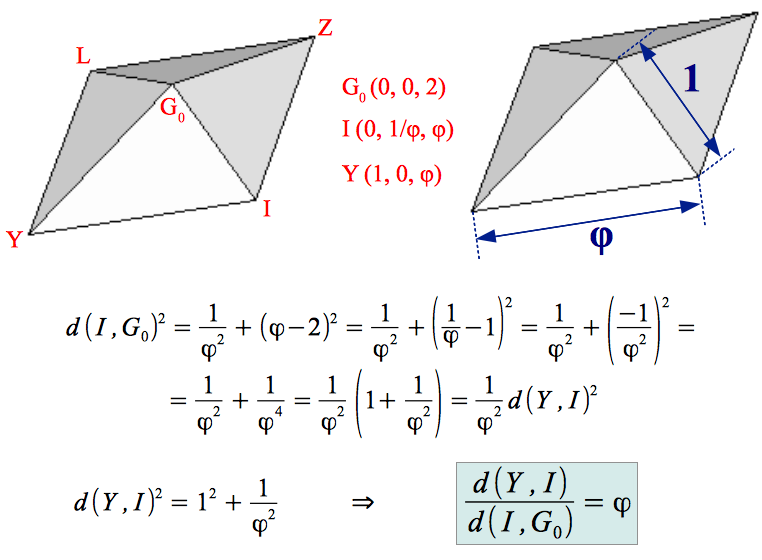
6.- About structural stability
The polyhedra that we have examined in this article follow into two broad groups. To the first group pertain the tetrahedron, the octahedron and the cube. They have in common the fact that their cartesian coordinates have integer values. Therefore these polyhedra can be represented exactly in a computer. On the other hand, most of the polyhedra examined in this article pertain to the second group: the ones whose coordinates involve the Golden Ratio. These polyhedra cannot be represented exactly in a computer. The coordinates that we have used for our plots are accurate to ten decimal places, but the Golden Ratio has an infinite number of decimal places. This fact does not (impide) their exact physical construction. For example the icosahedron can be constructed with a set of thirty equal rods and twelve connectors.
If one attempts to build all those polyhedra, this will make evident that some of them are not structurally stable. The simplest example is the cube: if you have ever tried to build a cube with any kind rigid rods and rotating connectors, you may have noticed that it collapses. The same happens with the dodecahedron. Both of them can be stabilised by adding extra edges that connect their edges among them. For example the cube can be stabilised by joining its vertices with two interlaced tetrahedra (see Figure 1d), and the dodecahedron by joining its vertices from the interior in the form of a great stellated dodecahedron (see Figures 8 &9), or to the exterior forming a small stellated dodecahedron (see Figure 6). In any case, the resulting polyhedra does not "contain" the faces either of the cube or of the dodecahedron. From this observation, it can be conjetured that those structures might have a (subtle) energetic nature. A cube can be "seen" wherever a star tetrahedron is present, whereas the dodecahedron can be "observed" wherever an icosahedral structure is present -either a small or a great stellated dodecahedron. In fact, Buckminster Fuller already established that the necessary and sufficient condition for a physical construction to be structurally stable is that it must be triangulated -hence the stability of the tetrahedron, octahedron and icosahedron.
