- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Phi in the human body
1.- Introduction
Marcus Vitruvius Pollio, Roman architect (c. 25 B.C.), remarked a similarity between the human body and a perfect building: "Nature has designed the human body so that its members are duly proportioned to the frame as a whole." He inscribed the human body into a circle and a square, the two figures considered images of perfection. It is widely accepted that the proportions in the human body follow the Golden Ratio. In this article we will review some studies on the subject. We will show the nineteenth century findings of the Golden Ratio in the human body by Adolf Seizing, actually approximated by a Fibonacci sequence of measures. Then we will examine the Golden proportions of the human body proposed by architects Erns Neufert and Le Corbusier in the twentieth century. Finally we will show how a common study with a german and an indian population samples confirmed the presence of the Golden Ratio in some proportions of the human body.
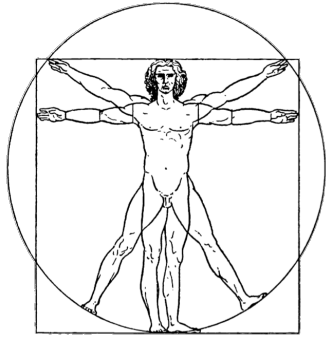
2.- Golden proportions in the human body found by Adolf Zeising
Adolf Zeising's main interests, back in the nineteenth century, were mathematics and philosophy. But after having retired he began his researches on proportions in nature and art. In the field of botany, he discovered the Golden Ratio in the arrangement of branches along the stem of plants, and of veins in leaves. From this starting point he extended his researches to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, etc., and finally to human and artistic proportions. The title of his first publication in 1854 declares his program: New theory of the proportions of the human body, developed from a basic morphological law which stayed hiherto unknown, and which permeates the whole nature and art, accompanied by a complete summary of the prevailing systems [1]. That universal law was, in efect, the Golden Ratio. There he presents his own proportional analyses of the human body (Figure 1).
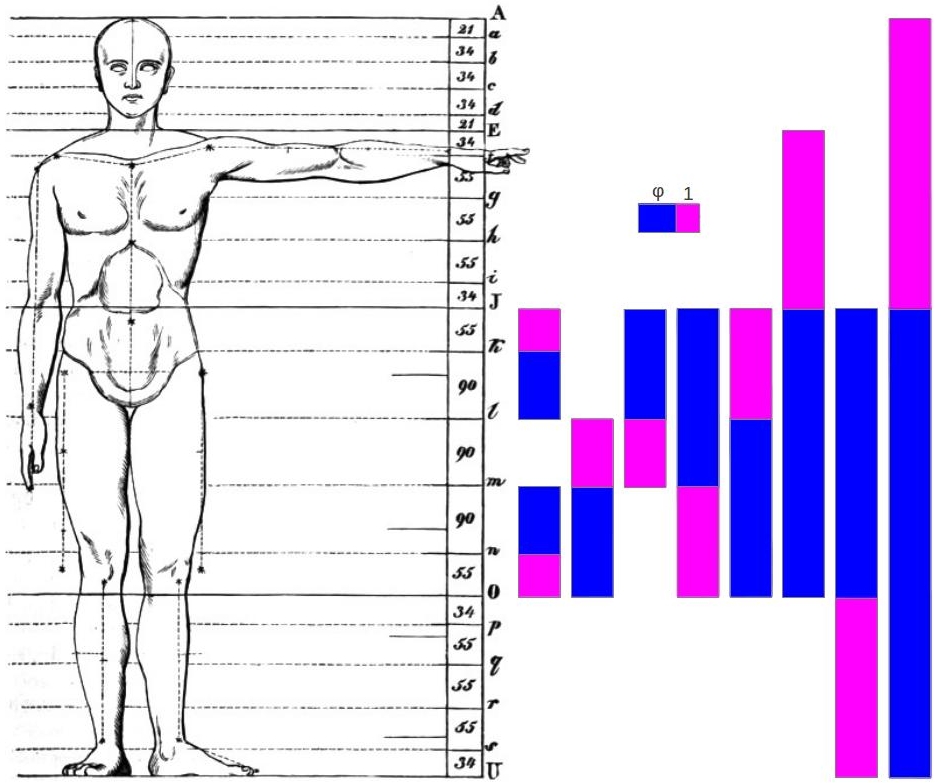 |
| Figure 1: Golden proportions in the human body found by Zeising [1]. |
Zeising divides the total height of a man's body into four principal zones: top of head to shoulder, shoulder to navel, navel to knee, and knee to base of foot. Each zone is further subdivided into five segments, which are arranged symmetrically within each zone: either following the pattern ABBBA or the pattern ABABA, but always summing up 2A+3B. By the way, the 3/2 proportion in each zone is a Perfect Fifth in the equal temperament musical scale. Is music involved in the design of our own body?
On the right of Figure 1 you can see the Golden proportions present in each of the segments, and between them, at different scales. Zeising's proportions of the human body are a beautiful example of how Nature closely approximates the Golden Ratio by means of a Fibonacci sequence of measures. Zeising erroneusly substitutes 90 for 89 in his measures, but we have used the exact value in the following calculations. The Fibonacci numbers present in his scheme, explicitly (green) or implicitly as grand totals (magenta), are the following:

Grouping consecutively each pair of adjacent measures one obtains an iterated division of the big segment (987) into consecutive Fibonacci numbers that closely approximate the Golden Ratio (Figure 2a). This reminds us the power of the Golden Ratio for consecutively dividing a segment with simple additions and substractions after the first split (Figure 2b). This sequence of Golden Ratio divisions also reminds us of the fractal nature behind the design of our body, because the same Golden proportion is repeated at all scales.
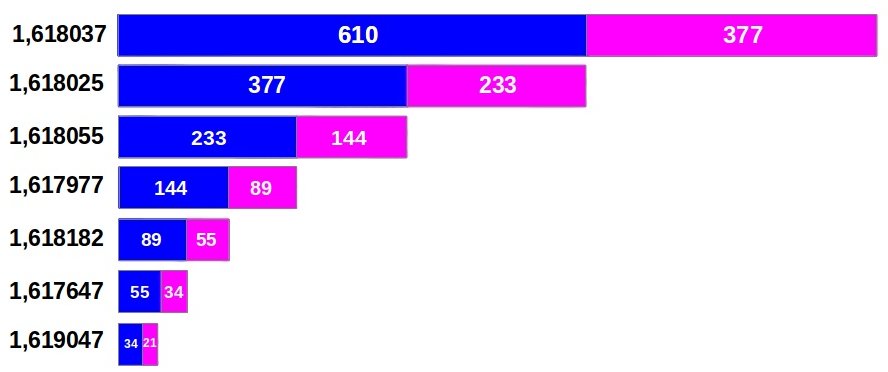 |
| (a) |
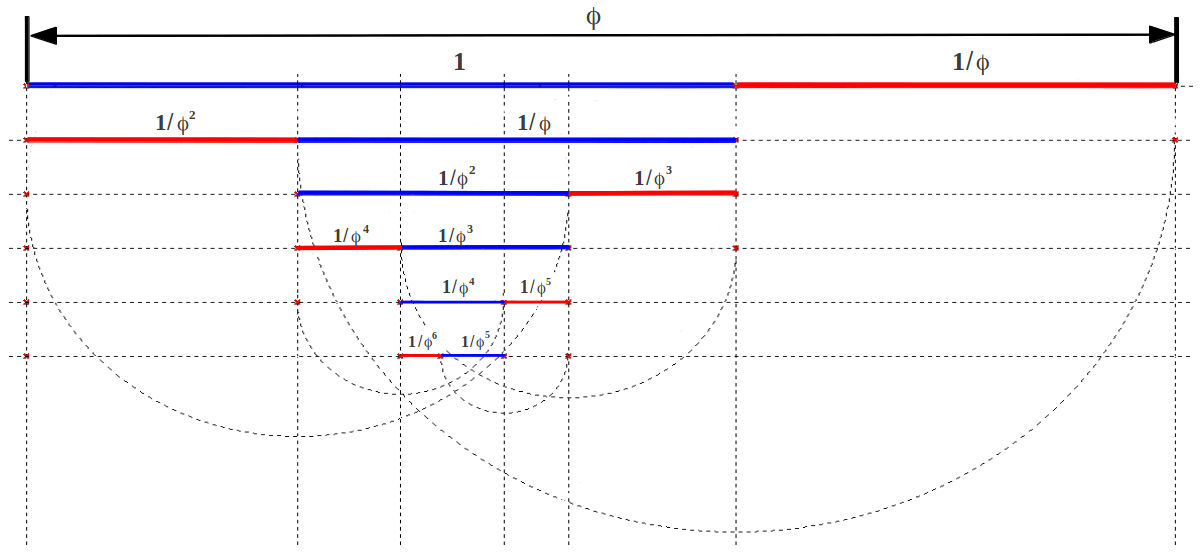 |
| (b) |
| Figure 2: Iterated division of a segment according to (a) the numbers in the Fibonacci sequence and (b) the Golden Ratio. |
3.- The Golden proportions proposed by architects Neufert and Le Corbusier
In the twentieth century the architect Erns Neufert (1900-1986) propagated the Golden Ratio as the architectural principle of proportion in the human body. Neufert did not strictly follow Zeising's human Fibonacci proportions, but introduces the exact Golden Ratio instead [2] (Figure 3). For him, the Golden section also provides the primary link between all harmonies in architecture.
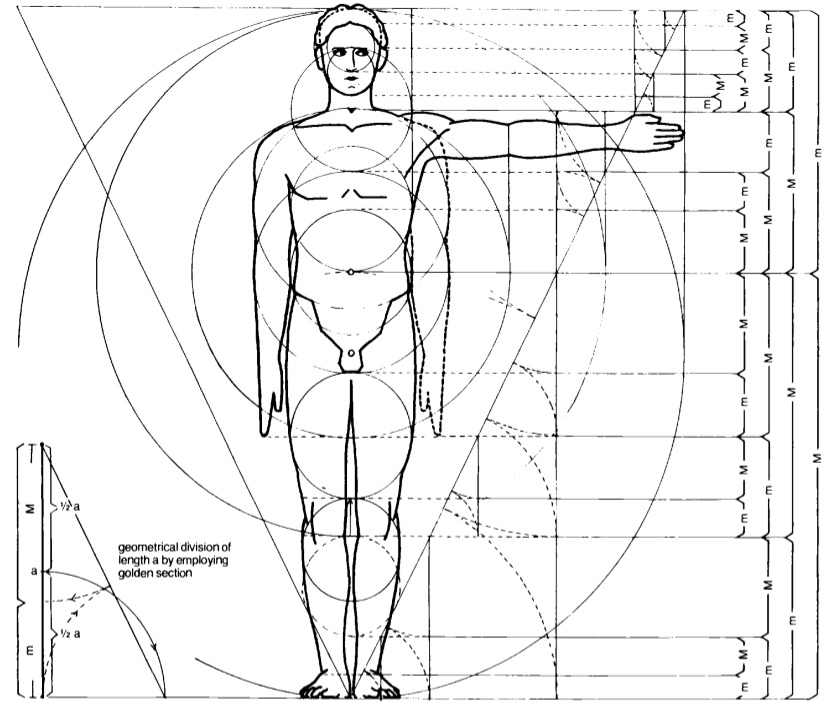 |
| Figure 3: Golden Ratio proportions of the human body after Ernst Neufert [2]. |
There is another great system of body proportions of the 20th century known as the Modulor, proposed by Le Corbusier (1887-1965). In his manifesto Vers une architecture, he presents the Golden Ratio as a natural rhythm, inborn to every human organism. For details on the historical origin and developement of Modulor I and II systems you can examine the excellent summary by architect Manel Franco [3]. Figure 3 shows the essential proportions proposed by Le Corbusier for the human body:
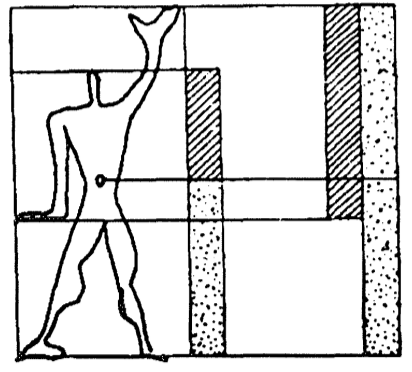 |
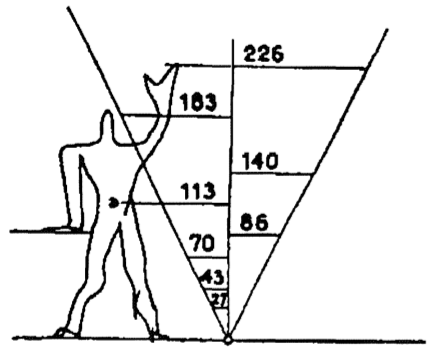 |
| Figure 3: Simple sketch and main Golden proportions in the human body proposed by Le Corbusier [3]. | |
In his final version, the Modulor II system proposes two Golden progressions of measures for the human body (Figure 4a). Returning to the style of Zeising, these progressions are actually two Fibonacci sequences of measures (Figure 4b). That is to say, each measure is obtained by the sum of the two preceding ones. Therefore, the ratio of any pair of consecutive values in these progressions closely approximates the Golden Ratio.
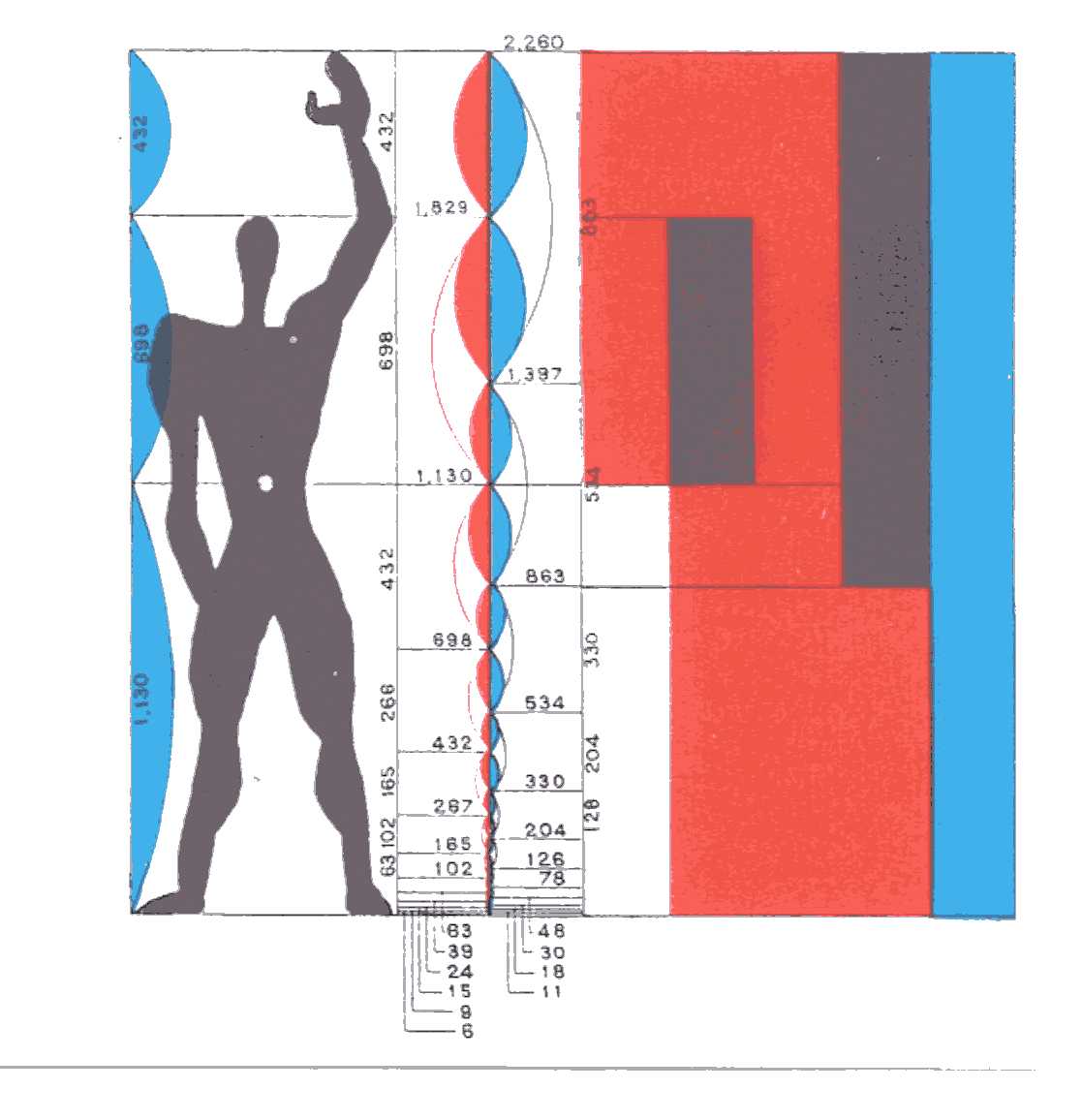 |
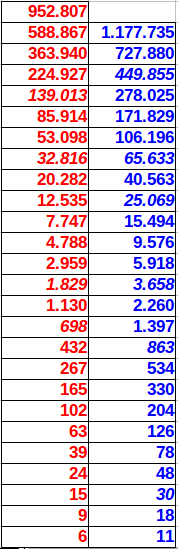 |
| (a) Golden proportions in the human body proposed in Le Corbusier's Modulor II. | (b) Detail of the red and blue progressions (in mm) in Modulor II. The ones in italic slightly deviate (1mm) from an exact Fibonacci sequence |
| Figure 4 | |
4.- A field study
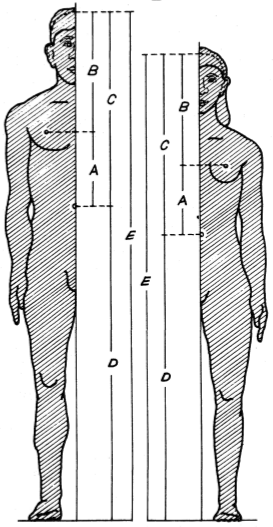
T. Antony Davis, from the Indian Statistical Institute (India) and Rudolf Altevogt, from the Zoologisches Institut der Universitat (Germany) conducted a study where they measured 207 german students and 252 youg men from Calcutta [4]. The measures taken A, B, C, D and E are shown in Figure 5a. In their results, they were able to confirm that the total height of the body and the height from the toes to the navel are in Golden Ratio (ratios D/C and E/D). Figure 5b summarizes their main results. They obtained the almost perfect value of 1.618 in the German sample (this value held for both girls and boys of similar ages) and the slightly different average value 1.615 in the Indian sample.
 |
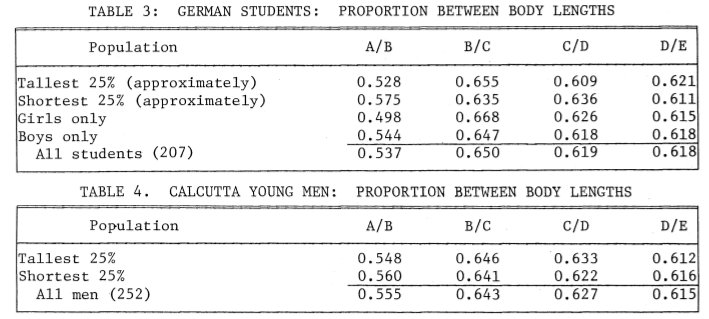 |
| (a) The measures taken in the study [4] | (b) Resulting average ratios, classified by population groups [4]. |
| Figure 5 | |
5.- References
[1] Zeising, Adolf: New theory of the proportions of the human body, developed from a basic morphological law which stayed hiherto unknown, and which permeates the whole nature and art, accompanied by a complete summary of the prevailing systems. (In German).
[2] Neufert, Ernst: Architects Data.
[3] Franco, Manel: El Modulor de Le Corbusier (1943-54)
[4] T. Antony Davis and Rudolf Altevogt, "Golden Mean of the Human Body".
