- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Metatron's Cube
1.- Introduction
I will try to provide a non conventional point of view of Metatron's Cube. This does not mean it is better or worse than others, it's just different. The aim is to deduce de three dimensional structure of the Cube.
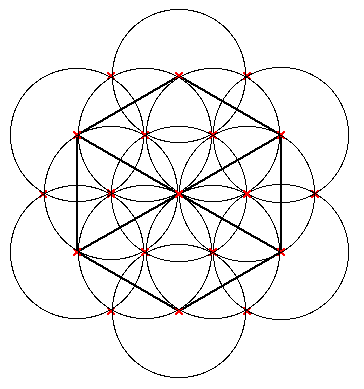
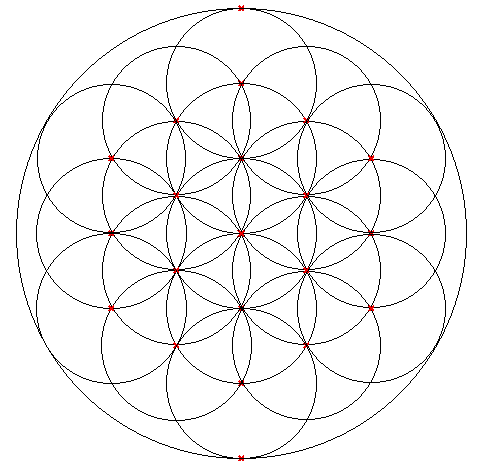
If you search information about Metatron's Cube, you will surely end up with the Flower of Life as a starting point to build the cube. The Flower of Life has 19 full circles inside, but there are 18 half circles which can be completed in outer direction. If you draw the flower yourself, you may not draw these half circles (see left figure below) because they would expand to the outer area:
 |
 |
| (a) Incomplete Flower of Life | (b) Flower of Life |
| Figure 1 | |
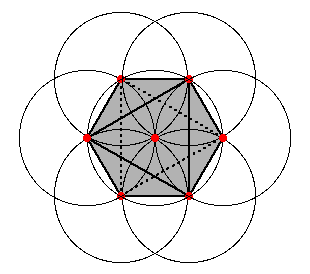
In any case, if you add or complete those missing circles and remove the two big outer circles, you end up with what I hold is the two dimensional representation of Metatron's Cube:
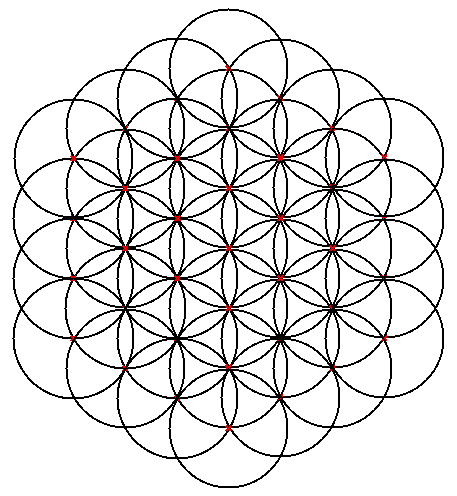 |
| Figure 2: Two dimensional representation of Metatron's Cube |
This figure can be seen as the two dimensional projection of a three dimensional cube made of 64 tangent spheres. I am conviced that this is the correct three dimensional representation of Metatron's Cube (actually the logo of our web page) and I will try to argue why in what follows.
| Figure 3: Three dimensional representation of Metatron's Cube. You can click on the image to see a true 3D model that you can zoom, rotate and pan. |
The two dimensional representation of Metatron's Cube that you can find elsewhere is formed from the Flower of Life, but with the completion of two layers of outer circles instead of one as we propose. One then ends up with a bunch of circles which is difficult to translate into a three dimensional figure. People use it to "show" that this enlarged grid seems to contain the five Platonic Solids and the Star Tetrahedron inside it (see this reference for further details). From that one could infer that the corresponding 3D cube should also contain those solids, something that I think is not true in all of the cases.
The objectives of this article are the following: to show how one can arrive to the preceding three dimensional representation of Metatron's Cube; to study the inner 3D grid that supports its spheres; to show that this grid supports the three dimensional construction of some solids at different scales (tetrahedron, octahedron, cube, star tetrahedron, ...) but not of others (such as the icosahedron or the dodecahedron); and to show where these solids are exactly located inside the Cube's grid.
2. - Where to start from?
After many hours of looking at the pattern of the Flower of Life and drawing a lot of drafts, one day I realized that the first hexagon in the pattern of the Seed of Life (the first seven spheres in the construction of the Flower of Life) could be seen as the projection of an octahedron (Fig.4). That was the first hint in the right direction:
 |
| Figure 4: The central hexagon in the pattern of the Seed of Life can be seen as the projection of a three dimensional octahedron. |
That made me think that the star tetrahedron, which is the stellation of the octahedron, could also be a building block of Metatron's Cube. In fact, the star tetrahedron is very important at many scales: it is the blueprint of our light body, the Mer Ka Ba, but is has also been recognised in the inner energetic structure of planets and stars.
 |
|
Figure 5: The inner grid of a star tetrahedron. It contains an octahedron in the middle, and eight tetrahedrons which stellate every face of this central octahedron. |
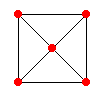
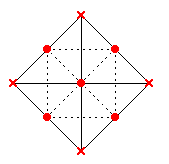
The following is a representation of an orthogonal projection of the octahedron (left) and the star tetrahedron (right) on the X-Y plane (seen from the top in the preceding figure). If the inner square lies in this plane (z=0) and the edge length is 1, then the upper and lower central vertices of the octahedron, and the outer vertices of the stellated octahedron have height z=.
 |
 |
| (a) XY view of an octahedron |
(b) XY view of a stellated octahedron |
|
Figure 6 |
|
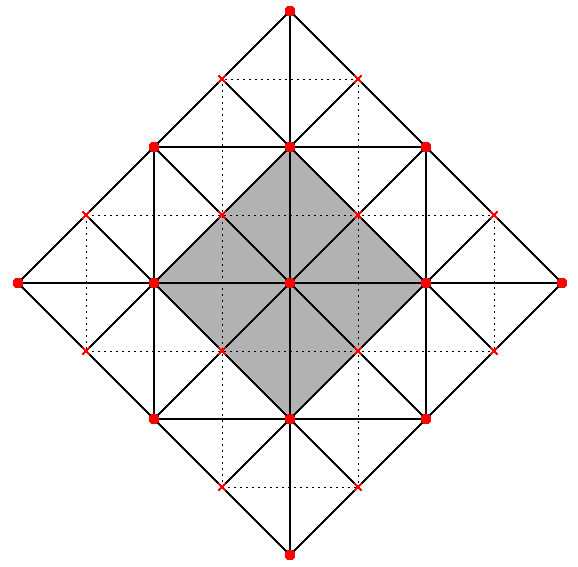
Lying strictly on the XY plane, the outer square of the projection of the star tetrahedron in Figure 6 seems to have grown out by a factor from the central square which represents the octahedron. This process can be further iterated a couple of times until we reach a size that can contain four star tetrahedrons. The side of the final square is twice the side of the original one:
 |
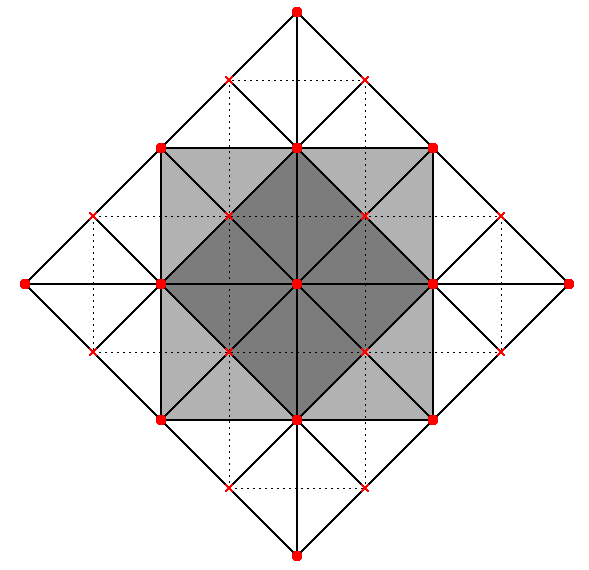 |
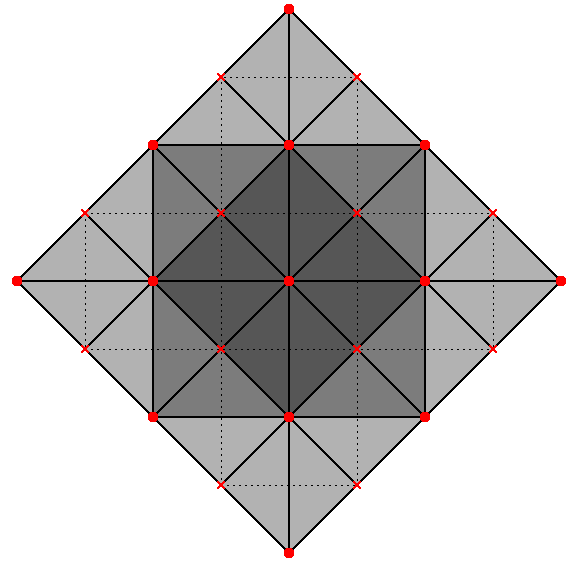 |
| (a) One star tetrahedron "grown" from a central octahedron. |
(b) Another iteration of growth. This intermediate stage has room for four octahedrons. |
(c) A second iteration now leaves room for four star tetrahedrons. |
|
Figure 7 |
||
3.- The inner grid of Metatron's Cube
The preceding growth pattern can be extrapolated to three dimensions. Let's put two star tetrahedrons side by side as in the following figure. If you look at the lower central part of the figure, you will notice that there is (half) a central star tetrahedron. So we see that a central star tetrahedron can be surrounded by four more star tetrahedrons, and each of them shares withg it two tetrahedrons.
 |
| Figure 8: Two star tetrahedrons side by side. |
Now the question is: how can this structure grow to become the three dimensional grid of Metatron's Cube? Our preferred alternative (there is another alternative that we'll discuss at the end of this article) is to stack a layer of four star tetrahedrons onto the preceding one, as in the following figure:
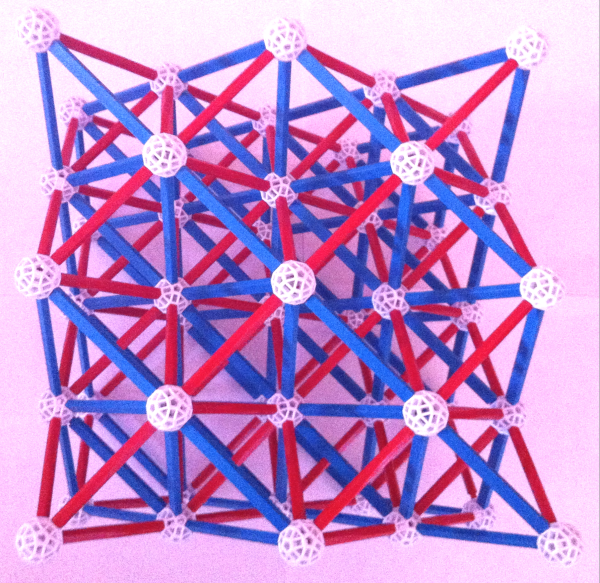 |
| Figure 9: Eight star tetrahedrons form the inner grid of Metatron's Cube |
I have come to the conclusion that this is the inner structure, the support grid of Metatron's Cube. We will see later that this structure contains other solids apart from its "biulding blocks", star tetrahedrons.
You can observe that this grid is symmetric: what you see from above is the same as you would see from any of the four sides and from below. The following figure shows an XY projection of the grid from which you can extract the coordinates of each vertex. The central octahedron in each star tetrahedron is shown in grey.
 |
| Figure 10: An XY projection of the inner grid of Metatron Cube. The structure has 4 vertical layers separated by a height times the edge size. |
4.- Where to place the spheres?
Now another question arises: where do we place the spheres? Because the number of vertices of this structure is exactly 63, an odd number. If we put a sphere on each vertex, we would end up with a three-dimesional structure very different from the pattern that the completed Flower of Life seems to suggest (see Fig.2). When one looks carefully to this grid, it can be appreciated that there are four tetrahedrons in between every group of three extreme vertices. We can see that in the upper layer, these add up to 16 evenly spaced tetrahedrons (Figure 9). And this grid is also found three times below the top one, so there are 64 evenly spaced tetrahedrons in this structure: exactly the number that we need to repoduce the three dimensional Metatron's Cube as shown in Fig.3!!
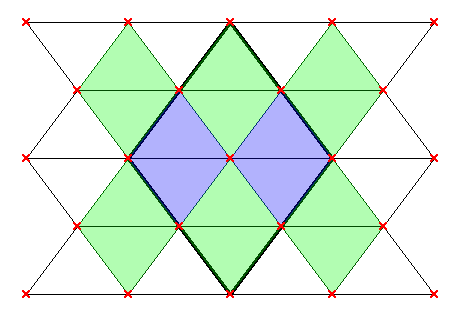
The physicist Nassim Haramein was the first to discover this grid. He calls it the "64 tetrahedron grid". In his recent documentary entitled "Black Hole" he explains the process that he followed until he decoded the grid. Haramein argues that this grid establishes the structure of the vacuum itself. The following figure shows two views the projected coordinates of the vertices of the grid (in red) and of the spheres (in green). Every sphere is located in the middle point of each tetrahedron:
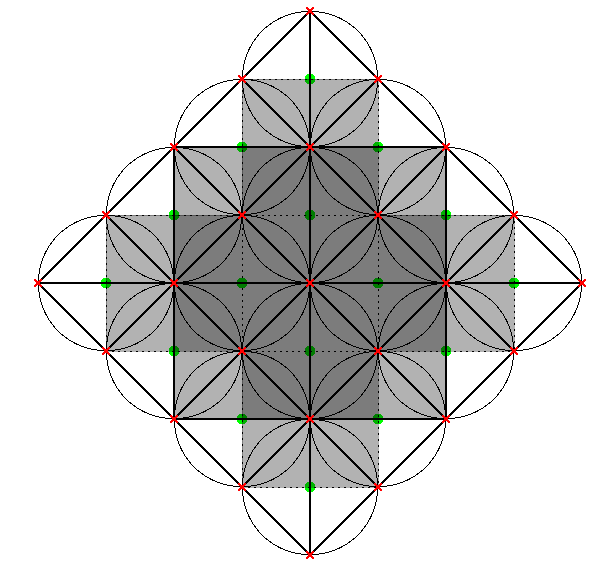 |
 |
|
| (a) XY projection of the inner grid of Metatron's Cube. Any pair of consecutive horizontal or vertical red points are separated by the edge length. The green circles indicate the center of the spheres. |
(b) XZ projection of the same grid (not to scale). Each pair of adjacent horizontal vertices are separated by the edge length, whereas each pair of vertical vertices are separated by |
|
| Figure 11 | ||
5.- Inside the grid
Now let's plug into the grid and see what solids can be found inside. The preceding figure suggests that there are several octahedrons, something that we already knew as this was our starting point. We can see in Fig.11 that there are exactly 14 small octahedrons in the grid, There is a central group of four, highlighted in violet in Fig.11b above, plus two layers of five above and below it, each one forming a cross, highlighted in green in Fig.11b above. The following figure shows some 3D views of this octahedrons grid:
 |
 |
|
(a) Central floor of octahedrons: front view |
(b) Central floor of octahedrons: top view |
The complete grid inside Metatron's Cube results from stellating all those octahedrons. Note that all of them share at least two tetraherons of their stellation with their neighbours.
Some of you may have noticed that the octahedrons grid shown in Fig.12c-e contains a big octahedron in its center. It is an octahedron with double edge length than its building blocks. Here you have a couple of 3D views of this bigger octahedron:
In order to obtain the full grid inside Metatron's Cube starting from this big octahedron, one must follow two steps: in the first step, you stellate the big octahedron, obtaining a big star tetrahedron that is also contained in the cube's grid (Fig.14a). After that, in a second step, you need to stellate the smaller octahedrons which compose each of the tetrahedrons that stellate the big central octahedron (Fig.14b). We could say that the stellation process is done in fractal steps at two different scales.
 |
 |
|
| (a) The big central octahedron can also be stellated (only one face shown) giving rise to a big star tetrahedron that is also present in the grid inside Metatron's cube. | (b) To obtain the full grid, one has to also stellate the small octahedrons in the middle of the big tetrahedrons that themselves stellate the big central octahedron. A fractal stellation! | |
| Figure 14 | ||
6.- In the core of Metatron's cube
Have you already guessed what is the structure that remains in the middle after removing all the outer peaces of the grid? Yes, it is a cuboctahedron, one of the Archimedean Solids. Strictly speaking, the structure contains a central vertex; it is what Buckminster Fuller called the vector equilibrium (Figure 15a). Quoting Maurice Starck "it is the only spatial configuration in which the length the polyhedral edges is equal to that of the radial distance from its centre of gravity to any vertex". So this structure is very significant. It has exactly 13 vertices: a central one, plus the outer ones that define 12 directions in space. I believe this structure is at the center of the life creating process (see our article on the Egg of Life).
Now we will see what happens when the vector equilibrium (from now on, cuboctahedron) structure grows in order to reach the complete grid inside Metatron's Cube. Actually what you have to do is to "expand" the original cuboctahedron adding an additional cuboctahedron at each of the 12 different directions in space. First you can add them in the 4 orthogonal directions found in the same horizontal plane (Fig.16a) and then in each of the 4 "diagonal" directions above and below (Fig.16b).
 |
 |
|
|
(a) Adding an cuboctahedron following one of the four horizontal orthogonal directions. |
(b) Adding a cuboctahedron following one diagonal direction, leading to the layer above (the same below). | |
| Figure 16 | ||
Do you guess what is the final result? Yes, you got it again: you end up with a big cuboctahedron (actually vector equilibrium) also contained inside the grid of Metatron's Cube. This cuboctahedron has double edge size than the preceding one. If we were talking of music, we would say that it sounds in the next octave. This big cuboctahedron has exactly 55 vertices, and contains 56 of the 64 spheres in Metatron's Cube. The following figure illustrates the square and triangular faces of this big cuboctahedron. To obtain the full grid of Metatron's Cube you simply have to add a tetrahedron to each triangular face, as shown in Fig. 14b above.
 |
 |
 |
||
|
(a) The triangular face of the big cuboctahedron of the next octave. |
(b) Another view of the triangular face. | (c) The square face of the big cuboctahedron of the next octave. | ||
| Figure 17 | ||||
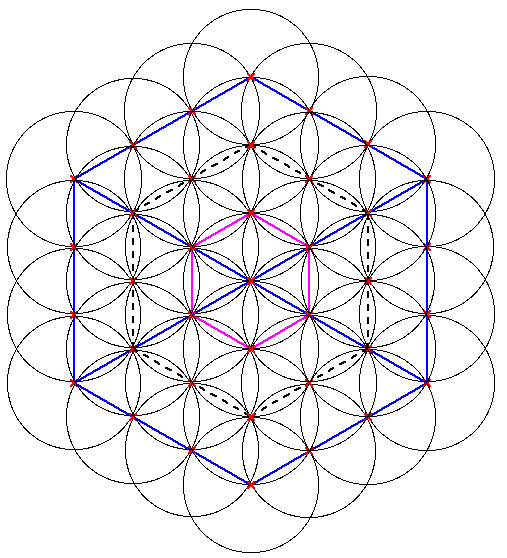
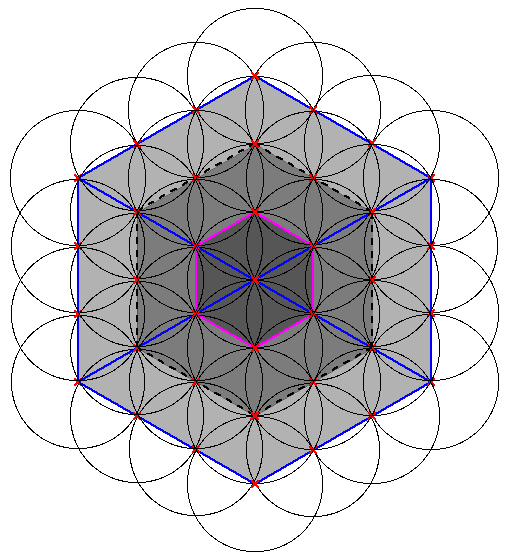
Notice that this fractal growth process could be iterated indefinitely. And not only in the outer direction (doubling the edge size) but also in the inner direction (halving the edge size). That's why Nassim Haramein calls the central point in the cuboctahedron the singularity. This fractal behaviour can be observed everywhere in Nature. The following figure shows that the Flower of Life pattern actually contains three iterations of cuboctahedron growth. As it often happens, things hide in plain sight:
 |
 |
|
|
Figure 18: Cuboctahedrons at three different scales contained inside the Flower of Life pattern. This fractal growth can be iterated idefinitely in the outer as well as in the inner direction. |
||
7.- Another alternative to the inner grid
I have discovered recently that the grid inside Metatron's Cube actually has two possible solutions. I have presented first the one which I think is the most likely. The other possible grid, although it also supports the centers of the 64 spheres, does not allow to build big Sacred Solids inside it.
The layer of four star tetrahedrons shown in Figure 9 can grow in a different way: instead of putting another layer of four star tetrahedrons on top of it, you can put half such a layer on top and half on bottom. Figure 19a shows this grid after completing it with half layer from below. Figure 19b shows the final alternative grid.
 |
 |
|
| (a) Completing a four star tetrahedrons layer with half such layer from below. | (b) The alternative inner grid for Metatron's Cube. | |
| Figure 19 | ||
Figure 20 shows a top view of the two grids. In our proposed grid, we can see a layer of four star tetrahedrons (Fig 20a). In the second one, there is a layer of five cuboctahedrons (Figure 20b).
 |
 |
|
| (a) Our proposed Metatron's Cube grid is composed of two layers of four star tetrahedrons one on top of the other. | (b) The alternative grid is composed of two layers of five cuboctahedrons one on top of the other. | |
| Figure 20 | ||
Notice that the alternative grid contains a central star tetrahedron instead of a cuboctahedron. Stated in another way, our proposed grid has grown from a central cuboctahedron (Figure 21a) whereas the alternative grid has grown from a central star tetrahedron (Figure 21b).
 |
 |
|
| (a) The proposed grid is made of two layers of four star tetrahedrons each grown from a central cuboctahedron. | (b) The alternative grid is made of two layers of five cuboctahedrons each grown from a central star tetrahedron. | |
| Figure 21 | ||