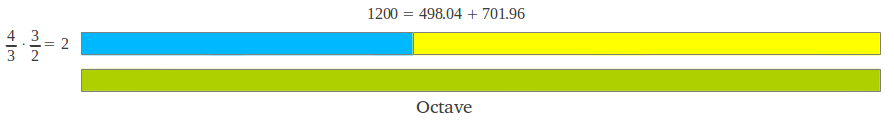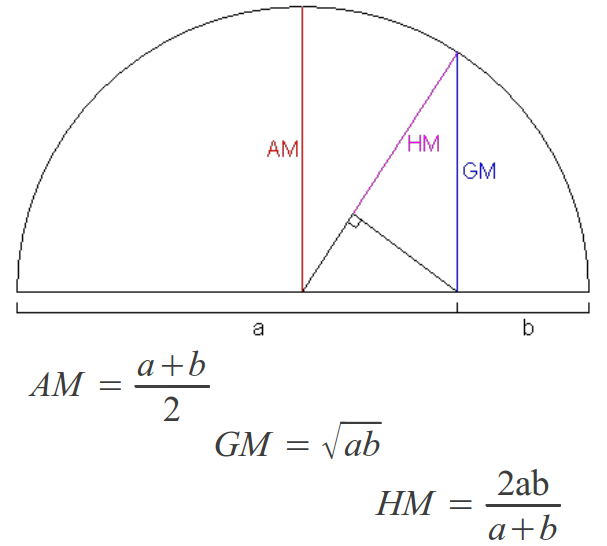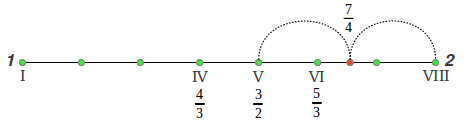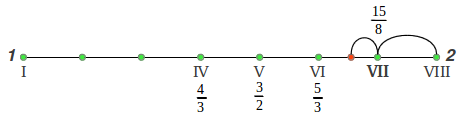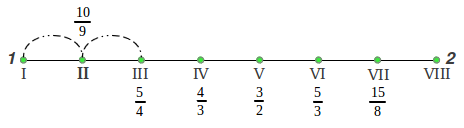- Home
- Golden Math
- Flower of Life
- Sacred Solids
- And much more...
- 3D Models
- 3D Flower of Life
- 3D Platonic Solids
- 3D Archimedean Solids
- 3D Catalan Solids
- 3D Deltoidal Hexecontahedron
- 3D Deltoidal Icositetrahedron
- 3D Disdyakis Dodecahedron
- 3D Disdyakis Triacontahedron
- 3D Pentagonal Hexecontahedron
- 3D Pentagonal Icositetrahedron
- 3D Pentakis Dodecahedron
- 3D Rhombic Dodecahedron
- 3D Rhombic Triacontahedron
- 3D Tetrakis Hexahedron
- 3D Triakis Icosahedron
- 3D Triakis Octahedron
- 3D Triakis Tetrahedron
- 3D Pyramids and Prisms
- 3D Stellations
- Phi in ...
- Sacred Solids in ...
- Music and Geometry
- About
- 3D Models
- Sacred Geometry and Energy
Proportion in Musical Scales
Table of Contents
1.- Introduction
2.- The Scale: Intervals and Ratios
3.- The "Pythagorean" scale
3.1.- Derivation of the diatonic scale
3.2.- Tetrachords and the seven scales
3.3.- Extension to a chromatic scale: The spiral of fifths (or fourths)
4.- Plato's Lambda and the three means
5.- The Equal Temperament scale
6.- The Just Intervals scale
6.1.- Derivation from arithmetic and harmonic means
6.2.- Comparison of scale intervals
6.3.- The scale intervals in the monochord
7.- The Greek Aulos Modes
7.1.- Historical background
7.2.- An alternative way to study the monochord
7.3.- Derivation from the harmonic mean
7.4.- The seven ancient Greek Modes
7.5.- The seven Greek Modes as subspecies
8.- The Scale of Twelve Fifths
8.1.- The scale structure and the formed fifths
8.2.- On the right concert pitch A=432Hz
9.- References
1.- Introduction
Some time ago, when I reproduced and extended some of Jean Claude Perez's research on the DNA, I found some musical intervals in several ratios of the codon populations of the DNA of the whole human genome (see this article). While trying to find some explanation to this findings, as I didn't have any musical knowledge, I started studying the structure of musical scales. I had learned from Robert Lawlor's excellent book on Sacred Geometry that musical scales are somewhat related to the geometric, arithmetic and harmonic means, but he didn't go any further into this subject. Besides the most widely known Equal Temperament Scale, I also felt attracted to what is commonly known as the "Pythagorean" tuning system. For my surprise, I discovered that this tuning system was not the one actually used by the Pythagorean school (it was later introduced by Aristoxenus). Pythagorean music was most likely based on the ancient Greek Aulos Modes, rediscovered and carefully documented by Kathleen Schlesinger, curator of old musical instruments in the British Museum, after having noticed that the finger holes of the Greek aulos appeared to be equidistant.
In the first part of this article, I will introduce the basic mathematical foundation behind musical scales so that anyone without musical knowledge as myself can understand their structure. Most books on musical theory focus on the arithmetic process, but the lack of a graphical support makes its study difficult. To help us compare different musical scales and understand their interval structure, I introduce a simple graphical method based on colours in which the intervals are drawn to scale. That eases the study enormously, and I hope it may be helpful to the trained musician as well. If you are a musician and find any mistake in my exposition, please let me know; I hope the figure below leaves you curious enough so that you keep reading... I'm going to show you how the structure of both actual and ancient musical scales can be easily derived from the three mathematical means (arithmetic, geometric and harmonic), and how the great diversity of musical intervals available in the ancient Greek Aulos Modes has been gradually lost from common musical practice. Finally, I will explain the structure of a new scale developed by musician Maria Renold, which combines the best of the ancient Aritoxenian scale and of the modern Equal Temperament Scale: the Scale of Twelve Fifths. This will allow us to introduce the fact that both the structure of the scale as well as the frequency to which it is tuned may have different effects on the human being, something that I suspect may be related to the geometrical structure of sound in three dimensional space. This subject will be further discussed in the second part of this article.
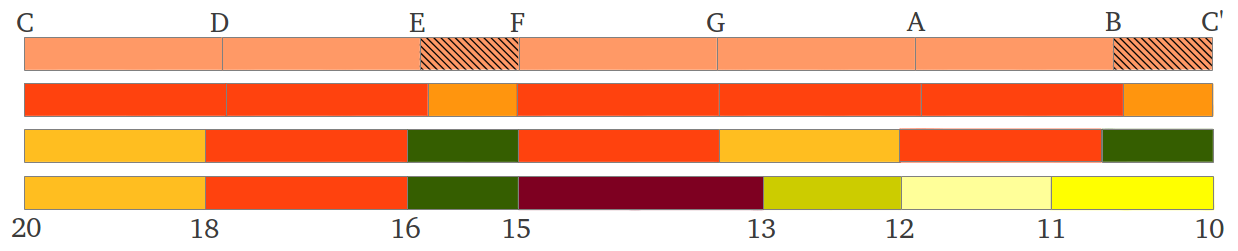
Modern and Ancient Diatonic Scales Compared
2.- The Scale: Intervals and Ratios
The basic musical interval is the octave, which contains an infinite number of frequencies between a reference frequency (the tonic) and its double. Scales partition the continuum of an octave into several chunks known as intervals. As a piece of music progresses, it uses intervals and combinations of intervals (chords) from this predefined subset. The structure of a given scale is the same in every octave. The number of intervals as well as the length of each interval in a scale are usually culturally determined. However, the set of all possible notes per octave is usually reduced to a very small number: seven notes in our diatonic scale, but up to 22 notes per octave in some Indian, Arabic or Turkish traditions [1]. Maria Renold highlights the octave and the scale as follows [2]:
"The octave is an exceptionally important interval in the musical experience of Western humanity. Many scales are contained within the octave, and all intervals, which we seek to understand here, are contained in such scales. Each scale which progresses from a keynote or prime to the octave, whether it ascends or descends, is heard by most people to be an organic whole -with careful listening, even the twelve-toned chromatic scale. The whole interval structure of a scale can thus be considered to be an organic structure with its own laws that proceeds from the octave."
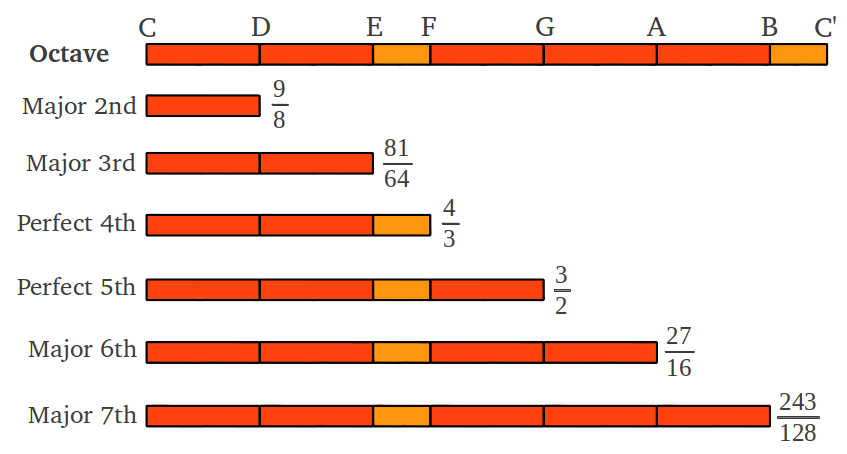
The seven notes in the diatonic scale, which correspond with the seven white keys in the piano, are usually numbered with roman numerals according to their position, from the first note, the tonic (DO=I) to the seventh note (TI=VII) up until the eigth note (DO=VIII) which is the first note in the next octave:

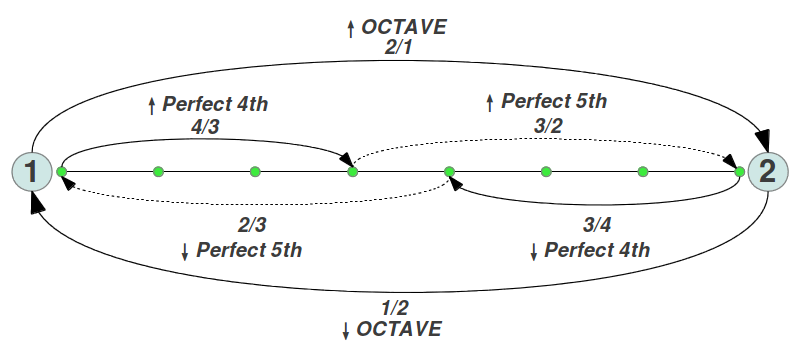
The length of an interval comprised between two notes of frequencies f1 and f2 is measured by their ratio f2/f1. The fourth note (FA=IV) is said to form an interval of a Fourth with the first note (DO=I). If the ratio of the frequencies of these two notes is exactly 4/3, they are said to form a Perfect 4th. Similarly, the fifth note (SOL=V) forms a Perfect 5th with the first note if their ratio is exactly 3/2. The remaining five notes from a perfect 4th up to the octave also form an interval of a Perfect 5th, because 2/(4/3) = 3/2. Therefore, the octave can be splitted exactly into two intervals of a perfect 4th and a perfect 5th (Figure 1). The intervals can also be formed in descending order (as the notes can be played accordingly), and in this case the ratios between their corresponding frequencies will be a number between 1/2 and 1, for example 2/3 for a descending Perfect 5th, and 3/4 for a descending Perfect 4th (Figure 1). The notes in an octave can be always represented by numbers between 1 and 2, provided we normalize the frequency of all the notes to the tonic (first note). Despite figures above and below may suggest the opposite, the length of each individual interval in the diatonic scale is not the same. We will shortly introduce a graphical method of representing each interval to scale, but we first need to introduce the measure of an interval in cents.
|
|
|
| Figure 1: An octave can always be represented by numbers between 1 and 2 provided that the frequencies of all its notes are normalized to the frequency of the first note. The octave can be exactly splitted in two intervals of a Perfect 4th and a Perfect 5th, either ascending or descending. | |
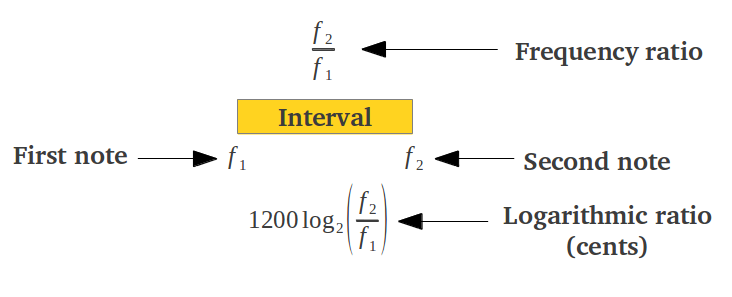
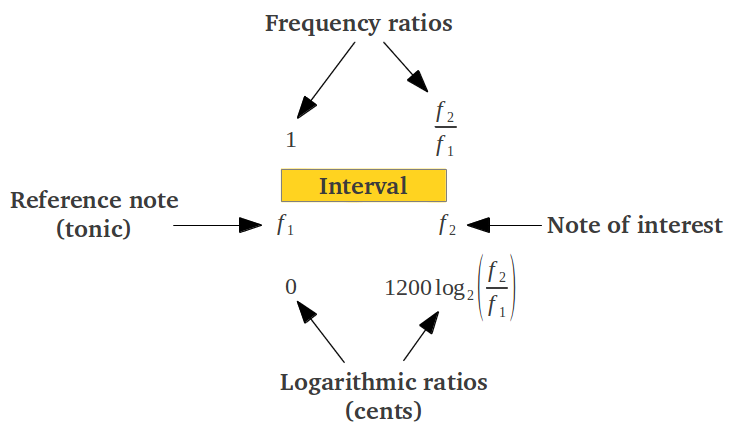
Working with integer ratios is not comfortable because they must be operated multiplicatively. For example to get the interval of an octave from the intervals of a perfect 4th and a perfect 5th, the individual ratios must be multiplied: (4/3) x (3/2) = 2. In addition, the musical intervals used in the modern Equal Temperament Scale do not correspond to exact integer ratios between their corresponding frequencies. Musical theorists have developed an alternative method of representing an interval that behaves additively and uses real numbers . The mathematical function that converts multiplication into addition in a natural way is the logarithm, as log(ab) = log(a) + log(b) and log(b/a) = log(b) - log(a). A musical interval f2/f1 is usually expressed in Cents according to the formula 1200·log2(f2/f1). In this way, an octave occupies exactly 1200 cents (Figure 2a). It is common practice to normalize all the intervals in an octave to the tonic (Figure 2b).
|
(a) |
(b) |
| Figure 2: Alternative representation of a musical interval as a linear ratio or in logarithmic cents, either (a) directly or (b) normalized. | |
The following figure shows several examples of intervals found in common musical practice both as an integer ratio and in cents. From now on, all the intervals will be drawn to scale, with a length proportional to the interval value in cents. This provides an easy way to add and compare intervals graphically.
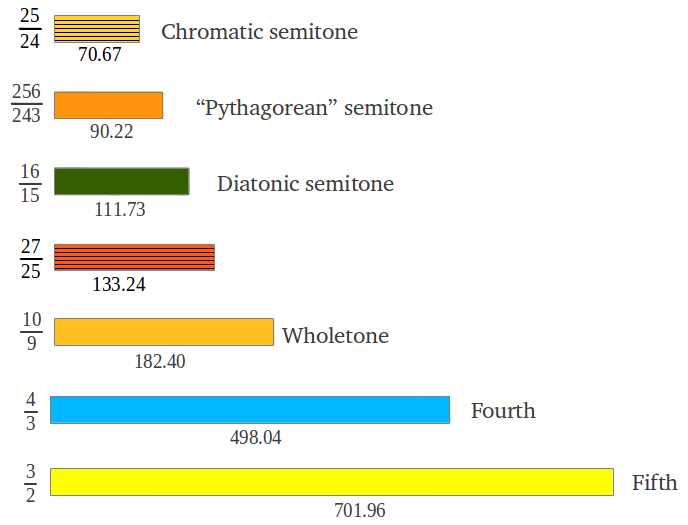 |
||
| Figure 3: Examples of some common musical intervals. The length of each interval is drawn to scale proportionally to its value in cents. |
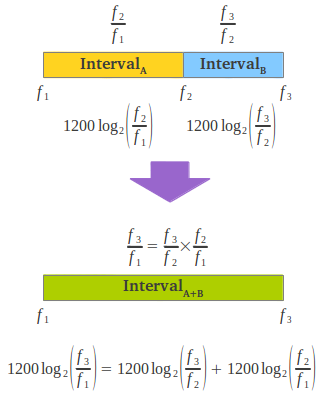
If two intervals are joined, the ratio of the resulting interval is the product of the ratios of each constituent interval. The logarithmic representation of musical intervals translates the multiplication of ratios to an addition of cents (Figure 4). Following our graphical representation, to get the result of the addition of two intervals one simply needs to put them side by side. Figure 4b contains examples of addition of some of the intervals shown in Figure 3 above.
|
(a) |
(b) |
| Figure 4: Three notes define two musical intervals that can be joined either multiplicatively or additively in cents. | |
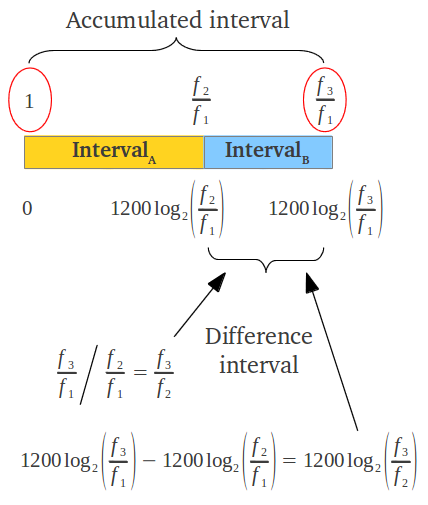
When one needs to draw more than one interval simultaneously, as it happens when we are representing the seven notes in a diatonic scale, it is common practice to substitute each note with the accumulated interval from the tonic to that note. This operation in equivalent to normalizing (dividing) the frequency of each note by the frequency of the tonic (Figure 5a). In this case, the ratio of any of the individual intervals can be obtained by dividing the accumulated ratios of the two notes that form the interval, or alternatively subtracting their equivalent values in cents (Figure 5).
|
(a) |
(b) |
| Figure 5: Each note in a joint representation of several intervals is usually normalized to the tonic. Thus the corresponding ratio represents the accumulated interval from the tonic to that note. Any of the individual intervals can be calculated either by dividing the corresponding ratios, or by subtracting their equivalent values in cents. | |
3.- The "Pythagorean" scale
3.1.- Derivation of the diatonic scale
The seven note Greek scale that has survived in written form was based on perfect fourths and fifths. This scale is elsewhere known as "Pythagorean" tuning, but it was actually introduced by Aristoxenus from the school of the Theorists in his 12 polemics, a written attack on the Pythagorean music system. Pythagoras and his pupils, who were known as the Harmonists, actually used the seven Aulos Modes described in a later section [3]. Therefore the Greek scale based on perfect fourths and fifths that we're going to describe should be properly called Aristoxenian scale. The basic premise of this scale is to contain as much Perfect fourths and fifths as possible. later on I will show how an ancient Chinese method allows the computation of the pentatonic (five notes) and heptatonic (seven notes) "Pythagorean" scales, both of which lack the eigth note: the octave.
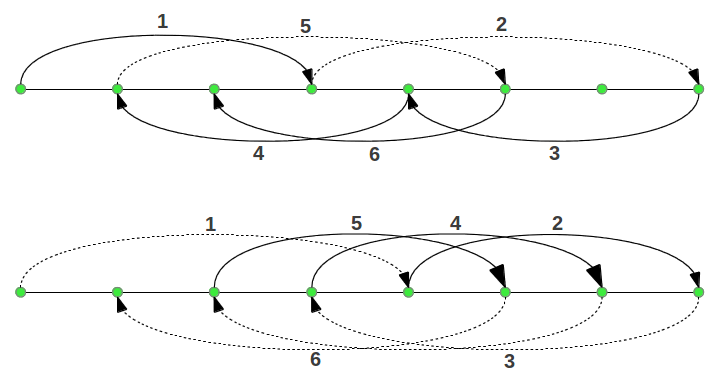
The length of all the intervals in this scale, including the octave, can be easily derived using six alternating "jumps" of a perfect fourth (an interval of four notes with ratio 4/3) or a perfect fifth (an interval of five notes with ratio 3/2), either ascending or descending, depending on the note where we want to "land". Figure 6 shows two different alternatives to do such jumps in order to complete all notes in the scale.
|
|
|
| Figure 6: Two possible ways of getting the eight notes of the "Pythagorean" scale with alternating jumps of a perfect fourth or a perfect fifth, either ascending or descending. |
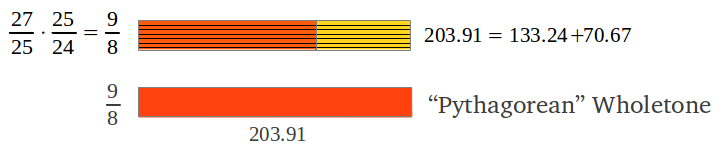
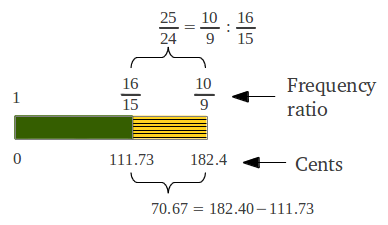
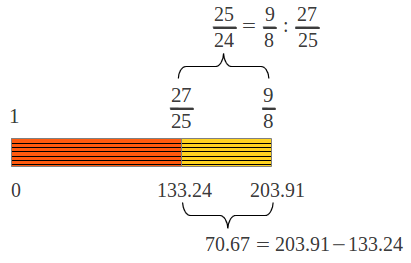
Each jump provides the accumulated ratio from the tonic to the "landing" note by multiplying the corresponding ratios (as described in Figure 1 above). For example if we follow the first sequence of jumps, the seventh note is arrived at in step 4, and its ratio is (4/3)·(4/3) = 16/9. The final result after the six steps of the first sequence is shown in Figure 7a. How many different individual intervals are there in this scale? In order to get the length of each interval one has to divide their accumulated ratios. The surprising result is that there are only two different interval lengths as shown in Figure 7b: that of a "Pythagorean" wholetone (9/8 or 203.91 cents, see Figure 4b), and that of a "Pythagorean" semitone (243/128 or 90.22 cents, Figure 3). The "Pythagorean" semitone is lower (in musical jargon flatter) than half a wholetone. Figure 7c shows the commonly accepted names for the seven notes in the diatonic scale (which can also be seen as accumulated intervals from the tonic).
|
(a) |
|
|
(b) |
|
 (c) (c) |
|
| Figure 7: (a) The accumulated ratio of each note in the "Pythagorean" scale after the first sequence of six steps detailed in Figure 6. (b) There are only two different individual intervals. (c) The commonly accepted names of each note in the diatonic scale; each note can also be seen as an accumulated interval from the tonic. |
It is important to observe that not all intervals of four consecutive notes form a perfect fourth. The perfect fourth contains two "Pythagorean" wholetones and one semitone. Any combination of two wholetones plus a semitone is called a fourth, but it need not be perfect (exact ratio of 4/3 or 498.04 cents) if any of its constituents varies its length: for example if one of the wholetones is shortened to 10/9 as it happens in the Just Intervals Diatonic Scale (see later). Similarly, a perfect 5th contains exactly three "Pythagorean" wholetones plus one "Pythagorean" semitone (exact ratio of 3/2 or 701.96 cents).
3.2.- Tetrachords and the seven scales
In the preceding figure we have introduced another common notation in musical practice, in which every note is assigned a letter from the set A-G. The assignment is not random: it is such that the interval E-F is the semitone located after two consecutive wholetones, and the interval B-C' is the semitone after three consecutive wholetones. The structure of this Greek scale was originally divided by Aristoxenus into two tetrachords separated by a middle wholetone (Figure 8).
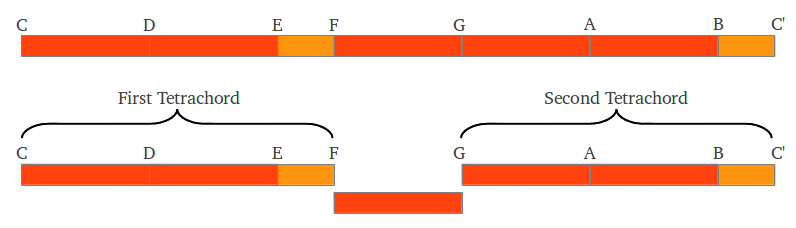 |
|
| Figure 8: "Pythagorean" C Scale as two tetrachords. |
What would have happened if we had used the second set of six steps in Figure 6? Proceeding as above, the reader can check that the final result would be that shown in Figure 9. The total amount of wholetones and semitones is the same with a different distribution. The sequence of intervals is the same, but it starts with a "Pythagorean" semitone followed by three wholetones, so it is called E Scale.
|
(a) |
|
|
(b) |
|
| Figure 9: (a) The accumulated ratio of each note in the "Pythagorean" scale after the second sequence of six steps detailed in Figure 6. (b) The sequence of intervals starts in the E note. |
It can be appreciated that the E Scale of Figure 8b is actually a "circular shift" of the C Scale shown in Figure 9b. In fact, if we draw two consecutive octaves we can easily see that there are actually seven different "Pythagorean" Scales, depending on the note where the scale starts (Figure 10).
 |
|
| Figure 10: There are actually seven scales or modes in the diatonic "Pythagorean" scale, depending on which note the scale starts at. |
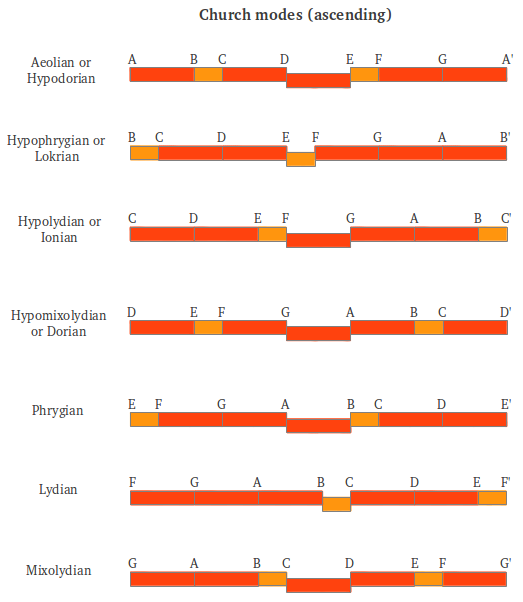
These seven scales, originally described by Aristoxenus in descending order, were also called modes, but they should not be confused with the early Greek Aulos Modes treated in a later section. Each scale was associated to a different planet according to Nichomachos, as well as according to the Ptolemaic view of the world (Figure 11a). The original names of the seven Greek scales were later converted into the ascending church modes and their names were erroneously mixed (Figure 11b).
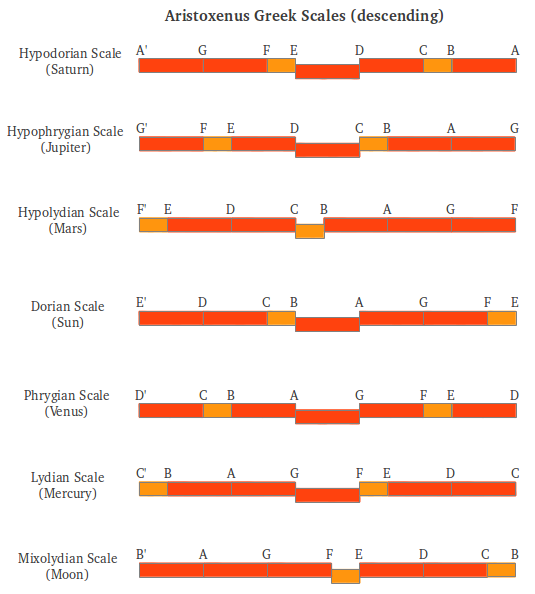 |
 |
|
|
Figure 11: The seven descending Greek scales, their association to planets and their later conversion into the church modes [2]. |
||
3.3.- Extension to a chromatic scale: The spiral of fifths (or fourths)
So far we have only considered the seven note diatonic scale, but most modern Western music makes use of a twelve-note scale known as chromatic scale. Is it possible to extend the "Pythagorean" diatonic scale to a chromatic scale? In order to answer this question, I will make use of an ancient Chinese method of computing the "Pythagorean" pentatonic scale, which can be extended to an heptatonic and finally a twelve-note scale. The procedure can be found elsewhere as "The spiral of Fifths", although it is far easier to understand if we use the complementary interval of a fourth.
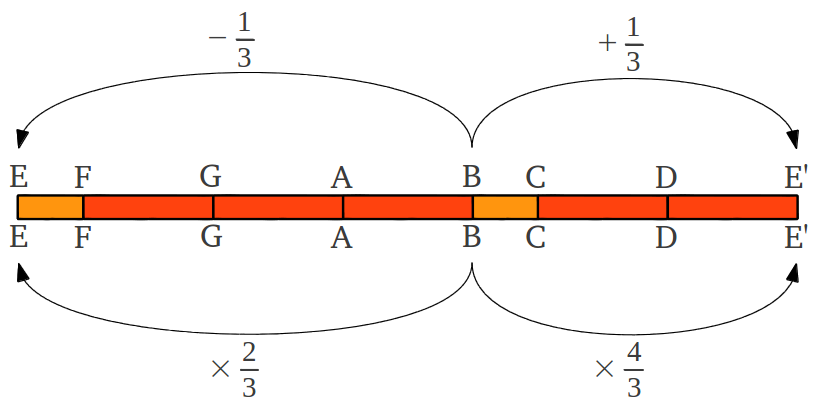
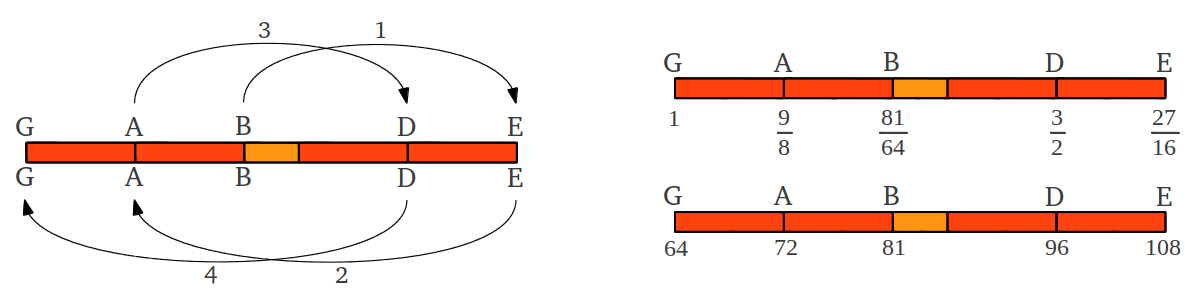
The rule is known as "add or subtract one third", and its oldest expression is attributed to Kuan Tzu (7th century B.C.) who explains how to apply it arithmetically and geometrically to generate the pentatonic scale [4]. One must start with "three four times", that is 3x3x3x3=34=81, and apply the rule until the powers of 3 are exhausted. The first step would be 81+81·(1/3)=108=33·22; the second step, 108-108·(1/3)=72=32·23; the third step 72+72·(1/3)=96=3·25; and the fourth and last step 96-96·(1/3)=64=26. The reader may be asking: and what does the sequence 81,108,72,96,64 have to do with music? Well, any of those numbers can be thought as a frequency, so to know how they are located in a musical scale -or how they are separated by intervals- we need to compute their ratios. Normalizing by the smallest number 64 and reordering we get 1, 9/8, 81/64, 3/2, 27/16. Do these ratios sound familiar? If we refer back to Figure 7, we see that on the C scale they are the sequence of notes C,D,E,G,A. Actually, the first one is the tonic or reference note, and the following four ratios are intervals: C-D (Major 2nd), C-E (Major 3rd), C-G (Perfect 5th) and C-A (Major 6th). Observing Figure 10, we see that the G scale shares the same starting interval structure with the C scale. In the G scale the sequence of integers 64,72,81,96,108 represent the notes G,A,C,D,E. Both scales provide us with the same cyclical sequence of five notes, which form the ancient pentatonic scale. Notice that any cyclical permutation of those notes would serve as well (D,E,G,A,C; E,G,A,C,D; or A,C,D,E,G).
The whole process can be better understood graphically (Figure 12). Adding one third actually means ascending a perfect fourth (4/3 = 1 + 1/3), whereas subtracting one third is equivalent to descending a perfect fifth (2/3 = 1 - 1/3). The sequence of notes G,A,C,D,E can be obtained starting from the B note and doing the four alternating steps of +1/3, -1/3, +1/3, -1/3 (Figure 12b).
|
(a) |
|
 (b) (b) |
|
| Figure 12: (a) The ancient rule "add or subtract one third" is actually equivalent to ascending a perfect 4th or descending a perfect 5th. (b) Application of the rule starting at B note generates the old pentatonic scale G,A,B,D,E after four steps, which can be numerically represented by the sequence of integers 64,72,81,96,108. |
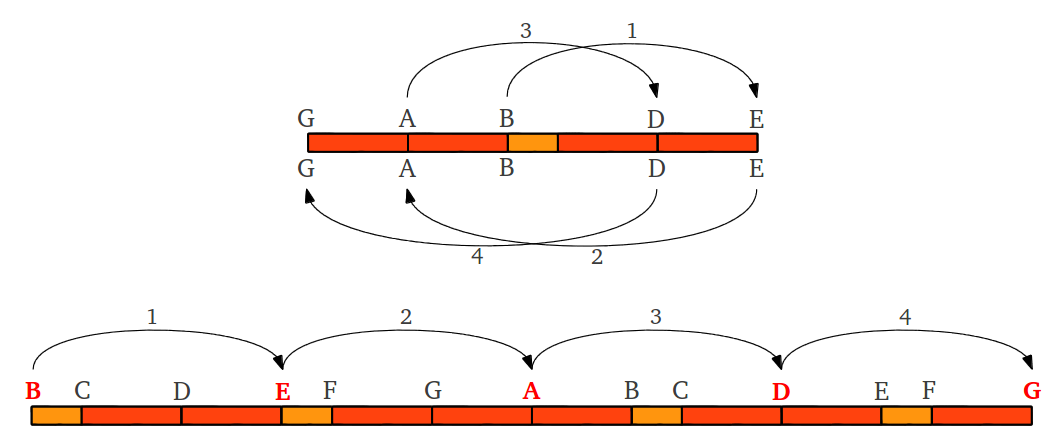
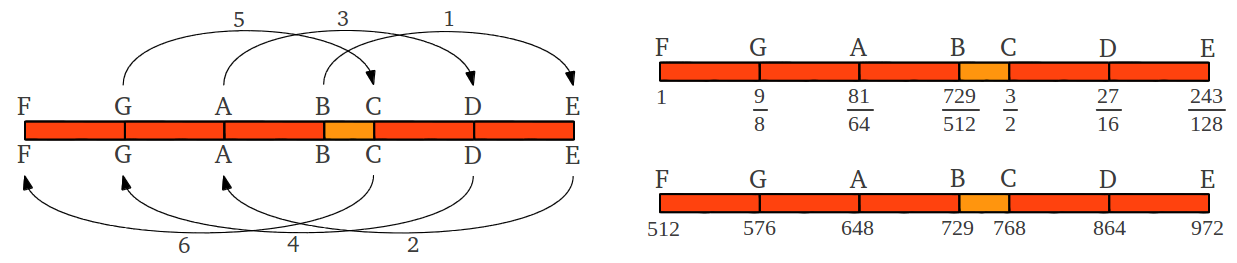
The simple rule "add or subtract one third" can be extended two steps further to generate the heptatonic scale, also known as Terpander heptachord (Figure 13).
 |
|
| Figure 13: Application of the rule starting at B note generates the heptatonic scale F,G,A,B,C,D,E after six steps. This scale can be numerically represented by the sequence of integers 512,576,648,729,768,864,972. |
The heptatonic scale scale contains all the inner intervals of the "Pythagorean" diatonic scale, except the octave!! This is a known limitation of the process of obtaining the notes exclusively by fourths (or fifths). In fact, descending a fifth is actually equivalent to ascending a fourth and transposing the resulting note down to the first octave dividing by 2. Therefore the alternating jumps of plus/minus one third can be substituted by positive jumps of +1/3 (ascending a perfect 4th) followed by successive division by powers of 2. This is illustrated in Figure 14 in the four step process that generates the pentatonic scale.
|
|
|
| Figure 14: Descending a fifth is actually equivalent to ascending a fourth and transposing down to the first octave. |
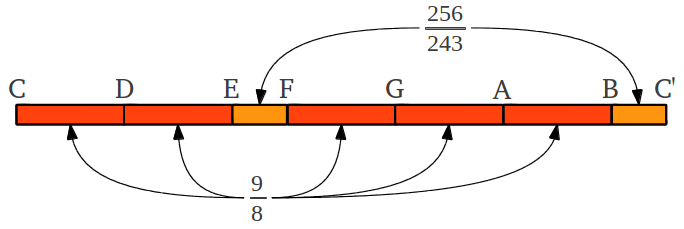
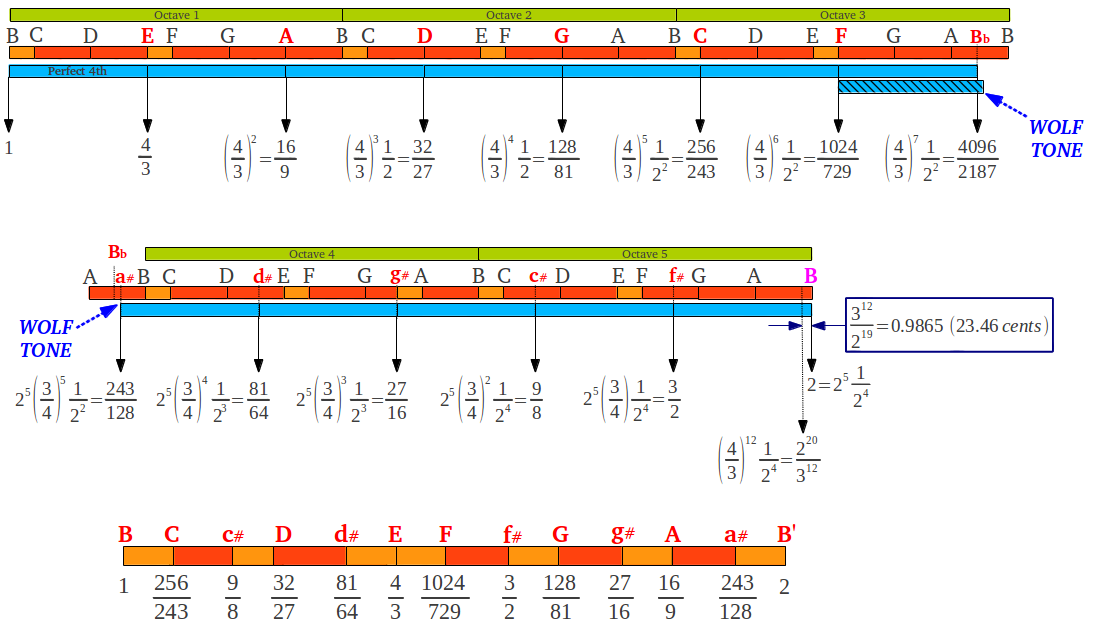
In order to get the twelve notes in the chromatic scale, this process can be iterated twelve times. However, after the sixth step one notices that the obtained ratios have increasingly big numbers, and that the final process does not end in a perfect octave. To overcome this problem, the seventh fourth can be slightly enlarged giving rise to what is known as the wolf tone, and this makes it possible to continue with perfect fourths and reach a perfect octave at the twelfth step (Figure 15). The error between the exact fifth octave and the one reached after 12 fourths is known as a "Pythagorean" comma (23.46 cents).
|
|
|
| Figure 15: Obtaining the "Pythagorean" chromatic scale from a sequence of fourths. To reach the fifth octave above without the error of a "Pythagorean" comma (23.46 cents), the seventh fourth is slightly enlarged leading to the Wolf tone at a#. The result is the "Pythagorean" chromatic scale in the B mode. |
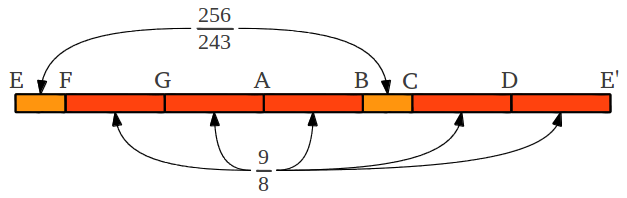
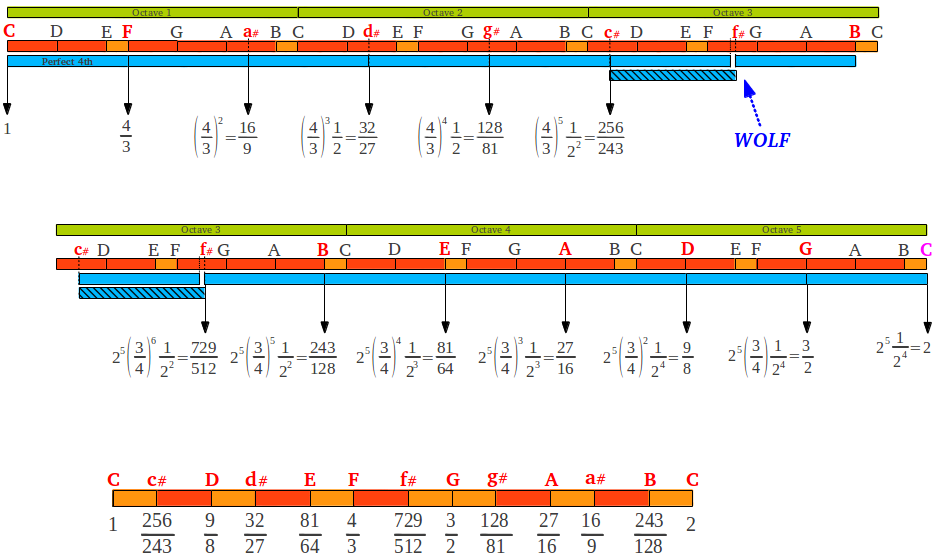
The wolf tone can be located at different notes, depending of the starting note in the process. In the following figure we show the same process starting with the more familiar C note. In this case the wolf tone appears on note f#.
|
|
|
| Figure 17: The "Pythagorean" chromatic scale in the C mode, with the wolf tone at f#. |
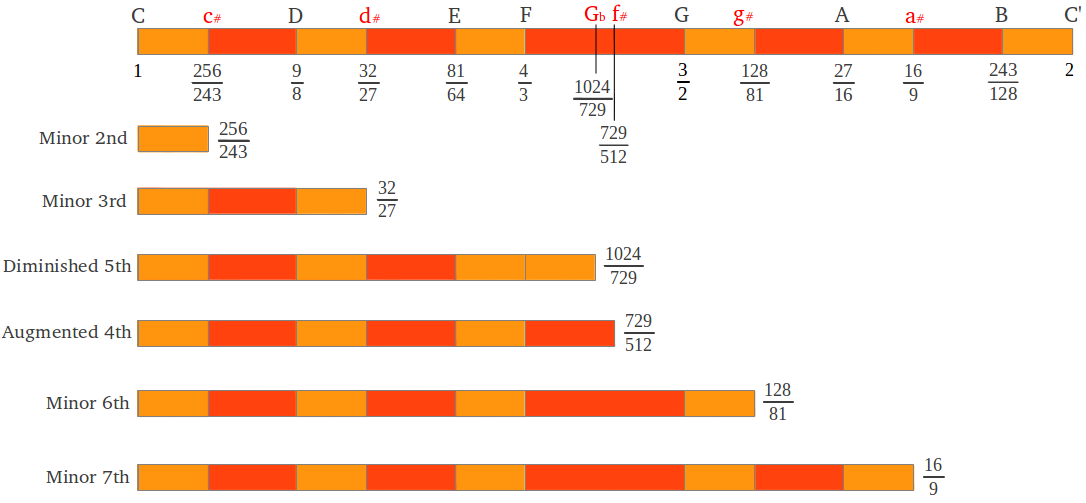
The five newly obtained notes would correspond to the black keys of the piano. The standard names are shown in Figure 18, where we can also see their corresponding intervals with respect to the tonic C. For seek of completeness, we show the two possible values of the wolf note: augmented fourth or diminished fifth. In the C scale they correspond to the two "Pythagorean" approximations of the tritone, a note located in the exact middle of the Equal Temperament Scale (see section 5).
 |
|
| Figure 18: The five extra notes of the "Pythagorean" chromatic C scale. |
Finally, I would'nt like to end the study of the "Pythagorean" scale without stating the importance of the number 3 in this scale. If we carefully analyse the ratios contained in the intervals of this scale, we can see that they are all based on powers of 3. Given a certain power of 3, either positive or negative, number 2 acts like a joker that allows us to transpose it to the 1-2 octave, converting an integer value to a fraction contained between 1 and 2. Figure 19 summarizes this analysis.
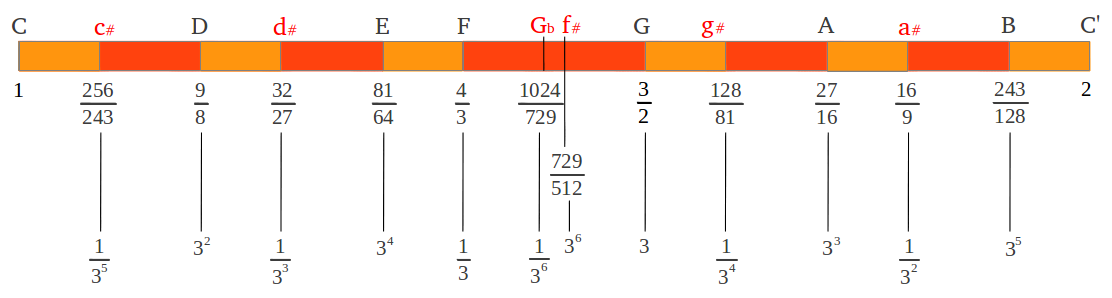 |
|
| Figure 19: The twelve intervals in the "Pythagorean" chromatic C scale as powers of 3. |
4.- Plato's Lambda and the three means
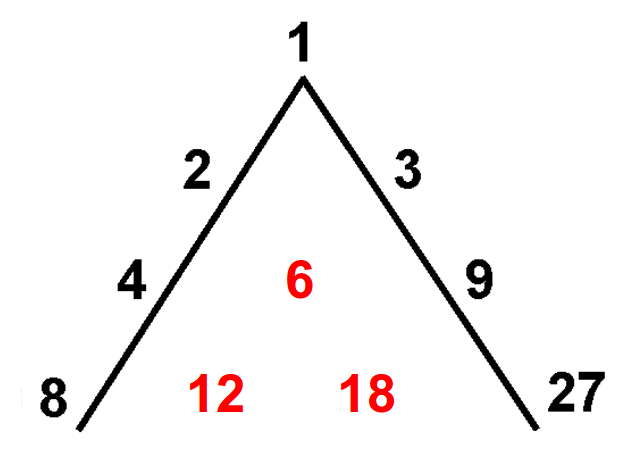
The famous disposition of the first three powers of numbers 2 and 3 known as Plato's Lambda (Figure 20a) will help us to introduce the three means (arithmetic, geometric and harmonic) in musical scales. The black numbers on the original Lambda follow a geometric progression, so each number is the geometric mean of the one before it and the one after it (for example 9=32 is the geometric mean between 3=31 and 27=33). The "completed" Lambda also contains the red numbers in the middle (6, 8 and 12) which be easily derived from their neighbours through the arithmetic and harmonic means. Figure 20b reminds us how to calculate the three means and how they are related to each other.
|
(a) Plato's Lambda |
(b) The three means |
| Figure 20: The black numbers in Plato's Lambda (on the left) follow a geometric progression, so each one is the geometric mean (GM) of the preceding and the following one. The red numbers can be derived through the arithmetic mean (AM) and the harmonic mean (HM) defined on the right. | |
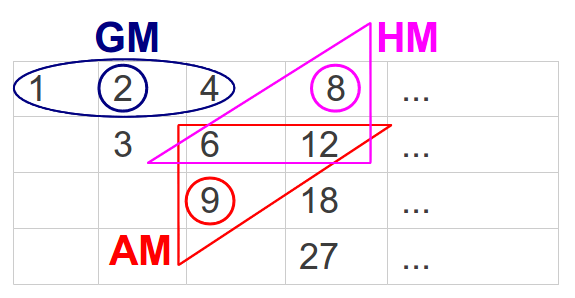
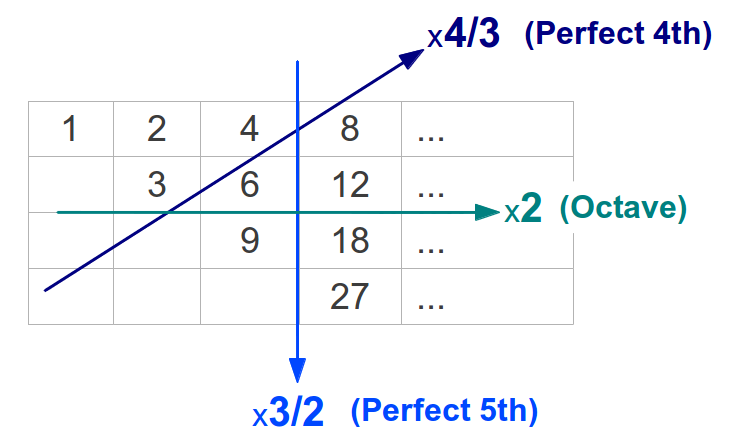
The relationship among those numbers and the three means can be better understood if they are rearranged into what is known as Nichomachos Table (Figure 21a). Each number in a row doubles its predecessor; this is true in the first row (powers of 2) as well as in any other one. Each number is the arithmetic mean of the two numbers above it, for example 9 = (6+12)/2, and the harmonic mean of the two numbers below it, for example 8 = 2·6·12/(6+12). The reader may be probably asking what does all this have to do with musical intervals: the explanation is provided in Figure 21b. There we can see that the numbers in Nichomachos table, taken in the appropriate direction, form the intervals of an octave (2), a Perfect 4th (4/3), and a Perfect 5th (3/2).
|
(a) Nichomachos Table |
(b) Musical intervals |
| Figure 21: (a) The numbers in Plato's Lambda can be arranged in the form of a table also known as Nichomachos Table. Each number in the table can be obtained as a geometric, harmonic or arithmetic mean of two numbers around it. (b) The numbers in Nichomachos table are also related through the most basic music intervals of a Perfect 4th (4/3), Perfect 5th (3/2) and an octave (2). | |
Let the numbers in the above tables represent the frequency of a note. Numbers 6 and 12 form an octave. The lowest note in the octave is usually referred to as the tonic. Numbers 8 and 9 are contained in this octave. Number 8 forms an interval of a perfect 4th with the tonic 6 because they are related by the ratio 8/6 = 4/3, and number 9 forms a perfect 5th with the tonic because 9/6=3/2. The interesting fact is that the perfect 4th ( in this example 8) is the harmonic mean of the two extremes of the octave (6 and 12), and the perfect 5th (in this case 9) is their arithmetic mean. Those are the two pillars of the "Pythagorean" scale discussed in the previous section. Figure 22 illustrates this in the usual 1-2 octave. In the following sections I will show you how these two means are also at the heart of the Just Intervals scale and of the ancient Greek Aulos Modes.
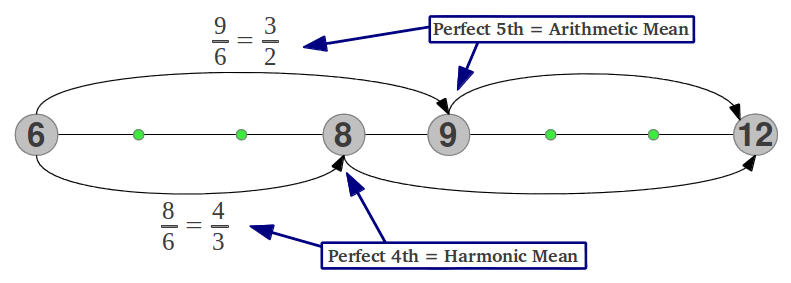 |
|
| Figure 22: Perfect 4th (Harmonic mean) and Perfect 5th (Arithmetic mean) |
5.- The Equal Temperament Scale
Before entering in the description and structure of ancient and more recent Just Intervals scales, let me introduce the modern 12-Tone Equal Temperament Scale (also called 12-tet), which is the tuning system used nowadays in most pianos. This scale is usually taken for granted today as universally used on keyboard instruments, but it is important to know that it did not exist in common practice on instruments until the early twentieth century. William Sethares [1] says that "many modern Western musicians and composers are even unaware that alternatives exist. This is not surprising, because most books about scales and musical harmony focus exclusively on 12-tet, and most music schools offer few courses on non 12-tet music, even though a significant portion of the historical repertoire was written before 12-tet was common".
The idea of Equal Temperament is very simple: the 12 notes in the chromatic scale are forced to sound an equal distance apart. That is to say, the scale is divided into 12 equal semitones. If the semitone has a "ratio" S and we want to reach the octave after 12 semitones, the equation that must be solved is S12=2, from which the "ratio" of each semitone must be the twelfth root of two, S=21/12=1.05946... Thus the "ratio" of the frequency between successive notes is no longer a ratio (rational number) but a real, irrational number. In the logarithmic domain the length of a semitone is exactly 1200·log2(21/12)=(1200/12)·log2(2)=100 cents. Following our graphic notation, figure 23 shows the 12-tet scale as well as the diatonic scale contained within it:
 |
|
| Figure 23 |
There are only three notes in the 12-tet scale which are related to one of the means introduced in previous section. They can be easily derived if one notices that the geometric mean of two intervals is equivalent to the arithmetic mean of their corresponding values in cents. Therefore, if we split the octave into a two halves (in cents) we obtain the tritone, and if we further split the two obtained halves into two, we obtain the Minor 3rd and the Major 6th. After that, three parts need be made of each interval to obtain the remaining eight notes, which is equivalent to perform the cubic root in the linear domain. According to Maria Renold "this may explain why to the ear the quality of the twelve intervals of this scale is completely different. The equal tempered tritones, minor thirds and major sixths are experienced to be genuine, while the equal-tempered fifths, fourths, major thirds, minor sixths, major seconds and both sevenths sound false [..] i.e. falsified to the human ear. This fact is commonly acknowledged [2, p.43]."
6.- The Just Intervals Scale
6.1.- Derivation from arithmetic and harmonic means
One critique of the Equal temperament Scale is that none of its intervals are pure, none of them is obtained by an exact integer ratio between two frequencies. For example, the fifths are each 700 cents, whereas a Perfect 5th (ratio 3/2) is 702 cents. In this scale, the imperfection of the wolf tone has been spread evenly among all the fifths. The Just Intervals Scale can be defined as the equivalent to the 12-tet scale made of pure, integer based intervals. Those intervals have ratios of small integers and this is why they sound consonant to the ear. People find intervals based on small integer ratios more pleasant because the ear naturally prefers small ratios. Galileo explained as follows [1, p.79]:
"Agreeable consonances are pairs of tones which strike the ear with a certin regularity; this regularity consists in the fact that the pulses delivered by the two tones, in the same interval of time, shall be commensurable in number, so as not to keep the eardrum in perpetual torment, bending in two different directions in order to yield to the ever discordant impulses".
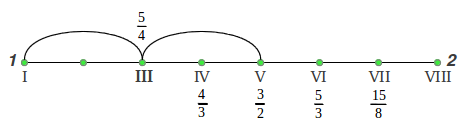
But which are the precise values of those pure ratios? It should not surprise us to know that, as it happened with the Perfect 4th and 5th, they can also be derived from arithmetic and harmonic means inside the octave, as was clearly shown by Maria Renold in chapter 7 of his excellent book, under the title "The form principles of the Just scales" [2]. The process is graphically illustrated in Figure 24. As we already know from section 4 (Figure 24a), the arithmetic mean of a rising octave 1-2 is the Perfect 5th (3/2), whereas its harmonic mean is the Perfect 4th (4/3). If we continue these divisions, the arithmetic mean between the fourth and the octave gives the just major sixth 5/3 (Figure 24b). The arithmetic mean between the fifth and the octave (Figure 24c) provides an intermediate tone not used in the scale (7/4), whose arithmetic mean with the octave provides the just seventh 15/8 (Figure 24d). The arithmetic mean between the fifth and the tonic gives us the just major third 5/4 (Figure 24e) and finally the harmonic mean between the just major third and the tonic provides the last note, the just major second 10/9 (Figure 24f):
|
(a) |
|
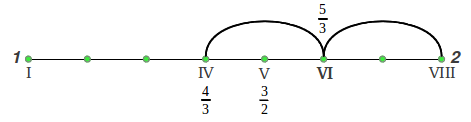
(b) |
|
|
(c) |
|
|
(d) |
|
|
(e) |
|
|
(f) |
|
 |
|
| Figure 24: The structure of the Just Intervals scale is obtained from the arithmetic and the harmonic means. |
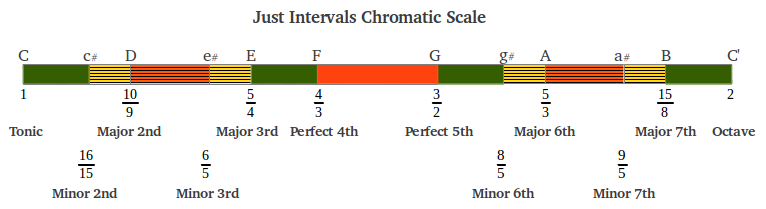
Figure 25 shows the length of the intervals in the Just Diatonic Scale drawn proportionally to their values in cents, as well as the pure ratios of the notes in this scale. It can be observed that there are only three different individual intervals within this scale with ratios 9/8, 10/9 and 16/15 (refer back to Figures 3 and 4 above). There is a small variant of this scale in which the two starting wholetones are interchanged (in that case, the major 2nd is the arithmetic instead of the harmonic mean between the just major third and the tonic).
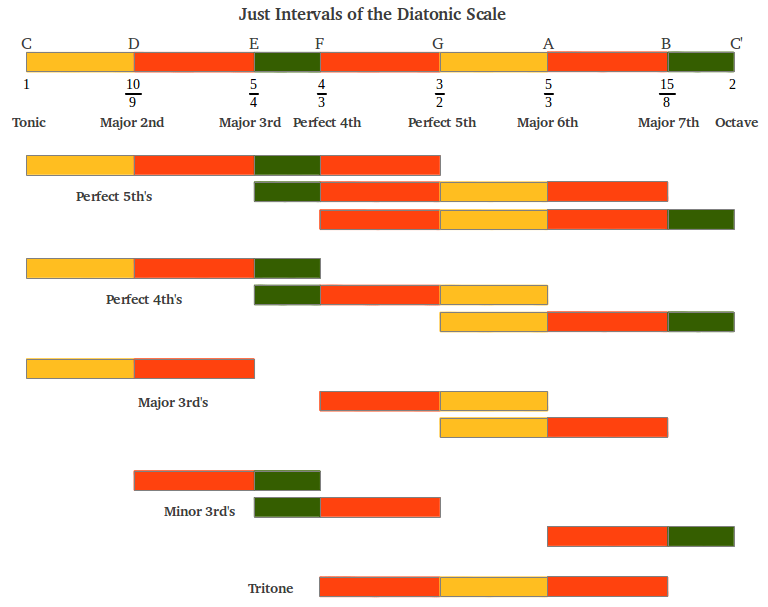 |
|
| Figure 25 |
The scale that we have obtained is actually known in today's music as the Major Scale. Musicians use also a Minor Scale, which corresponds to a shift of the tonic to the A note so that the major third becomes a minor third. The minor scale can also be obtained by arithmetic and harmonic means, although we are not giving the details here [2].
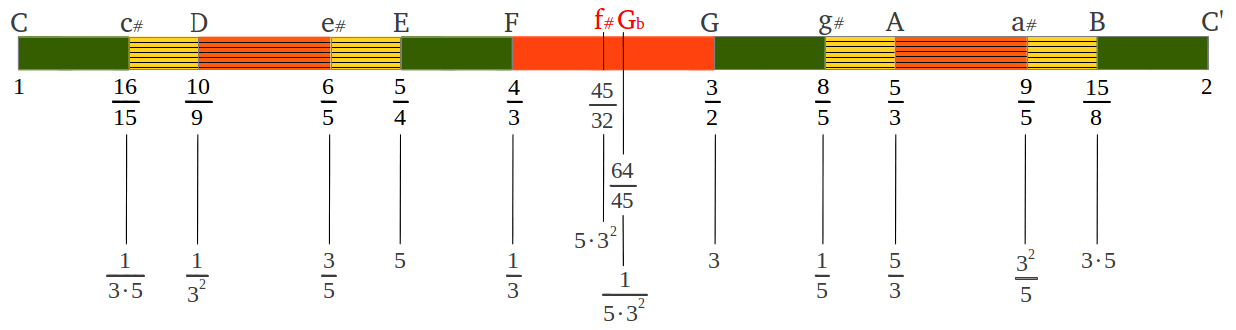
A Just Intervals Chromatic scale can be obtained by adding or subtracting a chromatic semitone to the appropriate notes of the diatonic scale (Figure 26a). This scale is worth several interesting observations. First of all, it is absolutely symmetrical, i.e. it has the same interval sequence both ascending and descending. This fact is also observable in the ratios of the intervals: for example the symmetric interval of the major third (5/4) is the minor sixth (8/5) because 2/(5/4) = 8/5. This also shows that those two intervals are complimentary, that is they add up to an octave as (5/4)·(8/5) = 2. Similarly, descending a minor third (6/5) places us at its ascending symmetric, the major sixth at 2/(6/5) = 5/3. It is also interesting to observe that the structure of hte Just Intervals scale has incorporated powers of number 5 to the powers of number 3 that were exclusively at use in Aristoxenus scale. We can see in Figure 26b that number five only appears raised to the first power, either in the denominator or in the numerator, and that powers of three have been reduced to the second degree. For seek of completeness, the just approximations to the equal tempered tritone, the augmented 4th and dimisished 5th, have also been included in the figure. Notice the crossover that has taken place in comparison with the same two notes in the "Pythagorean" chromatic scale (see Figure 19).
|
(a) |
|
|
(b) |
|
| Figure 26 |
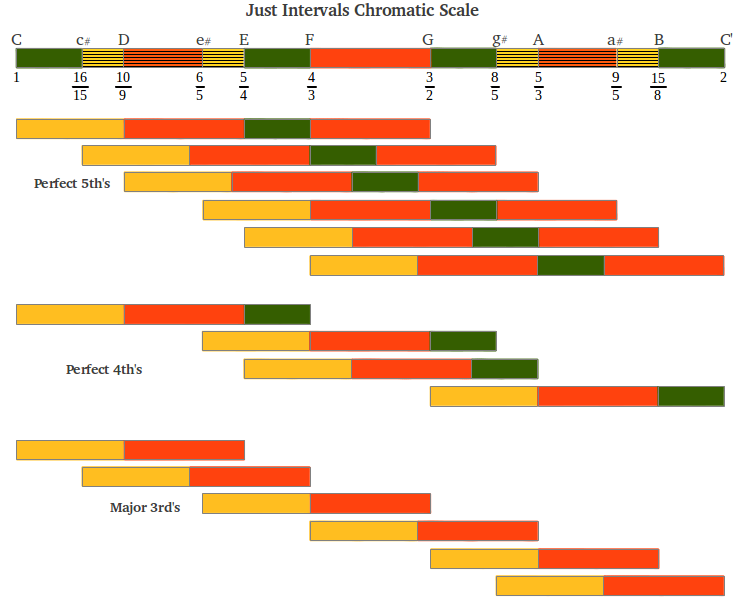
The just intervals contained within this scale are shown in Figure 27. It is clear that this chromatic scale contains many pure intervals within it. On the other hand, this figure allows us to see one inherent limitation of this scale, as far as modern polyphonic music is concerned. If we shift the tonic to the D note we would be playing in the D mode (sometimes also called the D key). But in that case the interval of a fourth would no longer be a perfect fourth, as it would contain two "pythagorean" wholetones, instead of one "pythagorean" and one chromatic wholetone. Therefore this fourth would sound different. The Just Intervals scale is often critisized because of this limitation: it is inherently key specific. William Sethares replies to this criticism as follows [1, p.62]: "Most advocates of Just Intervals (JI) do not insist that all music must necessarily be performed in JI. Simply put, if a piece does not fit well into the JI framework, then it should no be performed that way. Indeed, Just Intervals enthusiasts typically expect to retune their instruments from one JI scale to another for specific pieces."
|
|
|
| Figure 27 |
6.2.- Comparison of scale intervals
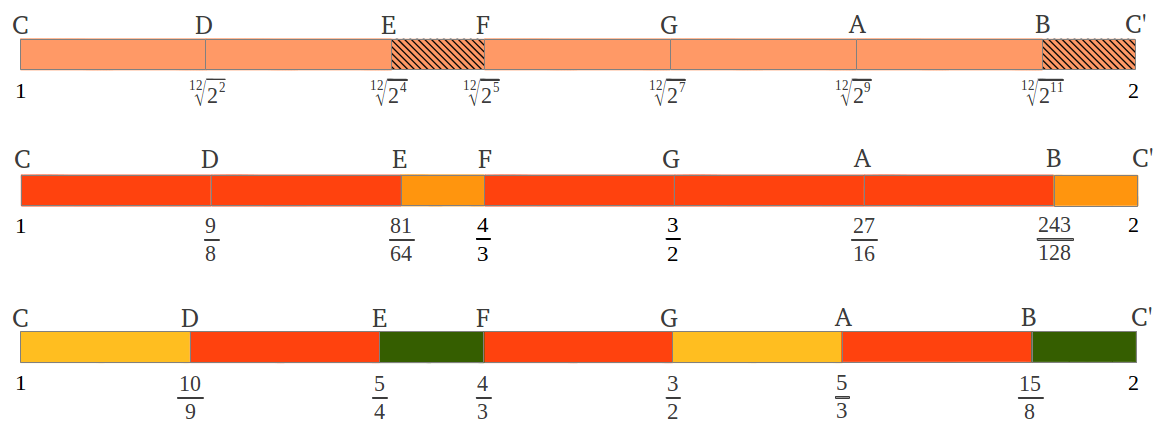
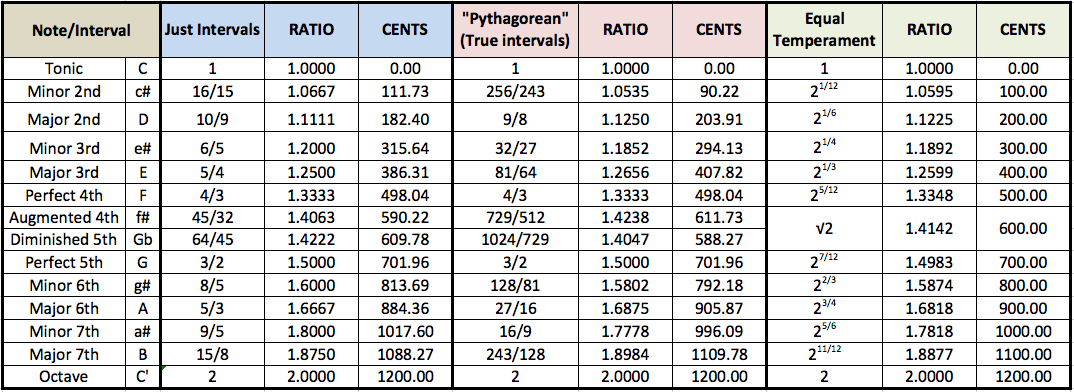
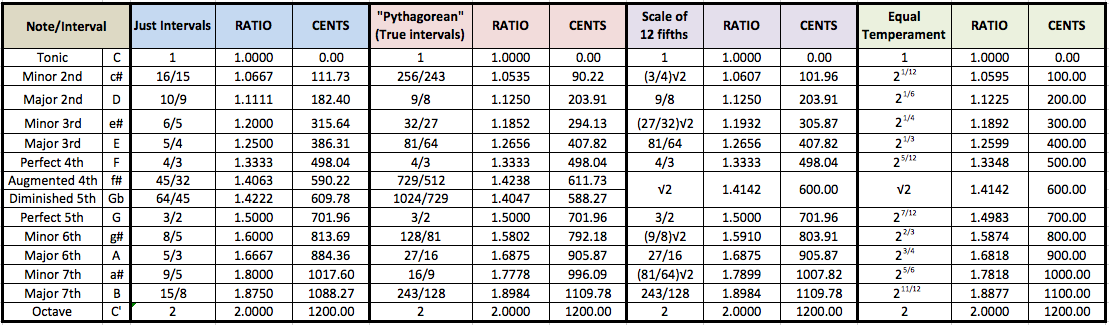
There are some differences among the intervals in the musical scales discussed so far, both quantitative and qualitative. The quantitative differences are graphically summarised in Figure 28a for the diatonic scales and in Figure 28b for the chromatic ones. The corresponding values in cents are compared in Table 1. Just Intervals and "Pythagorean" scales share the perfect fourths and fifths, whereas the seconds, thirds, sixths and sevenths are markedly different. It is curious to notice that "Pythagorean" intervals appear closer to Equal Tempered ones than Just Intervals. In a later section, we will see how Maria Renold combined the best of these two scales in her Scale of Twelve Fifths. What it seems obvious is that quantitavive differences among musical intervals, as the clear differences between just and true intervals, should translate into qualitative ones.
|
|
|
|
|
|
| Figure 28: Graphical comparison of Equal Tempered, "Pythagorean" and Just Intervals (a) diatonic and (b) chromatic scales. Quantitative differences appear in Table 1 below. |
 |
|
| Table 1 |
Maria Renold has spent many years of her life to the study and comparison of musical scales and intervals, as well as one of her deeply-felt questions concerning the correct concert pitch (reference frequency). Following her terminology, "Pythagorean" intervals are called "true intervals" (Table 1). As to the qualitative differences, she states the following [2, p.15]: "Intervals that are of different size and therefore of different quality are most widely used when playing music today [...] The qualitative difference between the just and true major thirds is that the former sounds peaceful, bright and courageous, but may also be felt to have an underlying sharpness. The latter beats a little but sounds as though it radiates light. The differences between the two minor thirds can be experienced in that the just minor third sounds beatless and sad, but with an underlying voluptuousness; on the other hand, the true major third sounds excited. A very unexpected and remarkable difference is found between the major sevenths. It is common knowledge that a just major seventh 15:8 with 1088.27 cents must be resolved into a neighbouring consonance, either upwards to the octave or downwards to the major sixth, if the ear is to be satisfied and the incredible tension is to be released. But the noticeably bigger true seventh 243:128 of 1109.78 cents although it obviously has a slightly dissonant character, sounds bright and peaceful, almost in suspension and exerts absolutely no compulsion on the human ear to be resolved. One can enjoy its brightness and beauty with equanimity and joy and let it resound unresolved."
6.3.- The Just Intervals in the monochord
The monochord is a simple "instrument" supposedly developed by Pythagoras to study musical frequencies and intervals. It consists of a resonating chamber, one to three piano strings, and in some cases a sliding bar or movable bridge that allows to select the string portion one wishes to play. This is shown in the following hand-made illustration by Elsie Hamilton [5]:
 |
|
| Figure 29: Monochord illustration by Elsie Hamilton. |
The string has a characteristic frequency which is inversely related to its length. When we play a string of length L, a standing wave is generated with a fundamental frequency proportional to 1/L. This wave propagates to the surrounding medium as longitudinal pressure wave, and if its frequency falls into the audible range (approximately between 20Hz and 20KHz) it can be heard by our ears. If the string is divided into two halves and one of them is played -by displacing the moveable bridge to the appropriate location in order to keep the rest of the string fixed- a frequency double the fundamental one is produced. This process can be iterated dividing the string length into three, four and more parts to produce all the integer multiples of the string's fundamental frequency, also called harmonics or overtones (Figure 30).
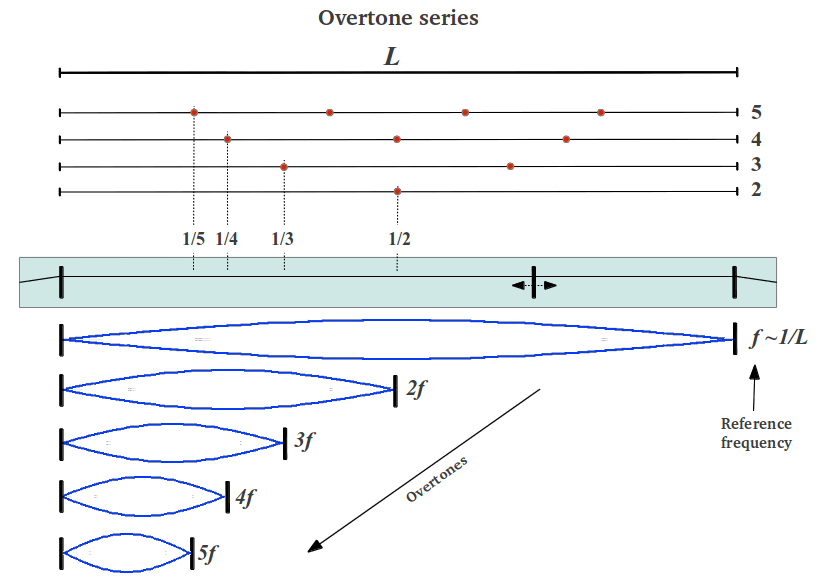 |
|
| Figure 30 |
This process can be generalised to produce sound frequencies which are related to the fundamental by any of the just intervals studied in this section (Figure 32): dividing the string into three parts and playing 2/3rds of its length produces a frequency 3/2 times the fundamental, which is a perfect fifth (playing 1/3 of the string length produces a perfect fifth but one octave above). Dividing the string into four parts and playing 3/4ths of it produces a frequency which is the perfect fourth of the fundamental. Similarly, a division of the string into five parts allows to generate the major sixth (3/5ths) and major third (4/5ths). Those unequally spaced marks in the monochord are the same that can be found in a guitar.
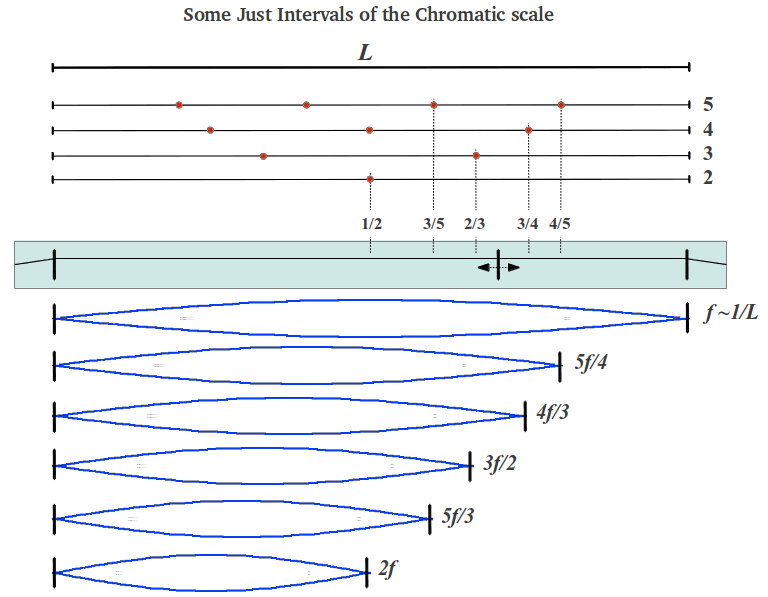 |
|
| Figure 31 |
7.- The Greek Aulos Modes
"Children, study your monochords"
(Pythagoras latest words)
7.1.-Historical background
When I started studying the structure of musical scales I felt attracted by the mathematical simplicity of the so called "Pythagorean" tuning method that I have explained in section 2. Almost everywhere you will find this scale attributed to our great Greek master Pythagoras, although no written record exists to confirm this fact. As clearly explained by Peter L.P. Simpson in his excellent review of the ancient Greek modes [3], the earliest written record on Greek music on which most scholars base their studies is known as the Harmonic Elements of Aristoxenus, a collection of books which survived largely intact. These books contain an attack and critique of those whom Aristoxenus calls the harmonists of the Pythagorean school, or in other words the modalists (because harmonia is the Greek for a musical mode).
Aristoxenus basically says [3] that the modalists did not understand the basics about music and did almost everything wrong. To correct their errors and to put the science of music on a sound footing, Aristoxenus throws out all the theorizing that was going on in his own day and replaces it with something new. Unfortunately, the something new he introduces has no place for the modes as traditionally understood. According to Aristoxenus, the way to understand music is to understand singing, and the way to understand singing is to start with the smallest consonant interval, namely the perfect fourth. The next consonant interval, the perfect fifth, produces, when joined to a fourth, the final consonant interval of the octave (according to Aristoxenus only these three intervals are consonant). All Aristoxenus’ scales, including his equivalents of the ancient modes -because he used the names of the modes for some of his scales- are constructed out of different kinds of tetrachords and their combinations (see Section 2).
The main critique to those historical facts is the following [3]: there is no necessary reason to base scales on Aristoxenan tetrachords, neither to construct tetrachords downwards -as Aristoxenus always did- neither to confine consonant intervals to fourths and fifths and octaves. Aristoxenus could, and did, appeal to the limits imposed by the capacity of the human voice, but there is no necessary reason to construct music, or its theorizing, according to those limits. Music is much richer in its possibilities than Aristoxenus allowed, but he excluded in his teachings any other possibility, presumably because he didn't actually understand what Pythagoreans were really doing.
The fact is that other Just scales exist besides the ones discussed so far. Quoting Maria Renold [2,p.27]: "Though hardly used in Western music over the last four to five hundred years, they have been known from ancient times and have been in use to this day amongst the people of Asia, Greece, the islands of Scotland, north America, etc. These scales, here called the seven Aulos Modes of ancient Greece, are called 'harmonai' by her rediscoverer musicologist [and Fellow of the Liverpool University Institute of Archaeology] Kathleen Schlesinger. As curator of old musical instruments in the British Museum she noticed that the finger-holes of the Greek aulos appeared to be equidistant. Thanks to her specific training she knew that such instruments could not produce the scales and intervals of today. The scales must therefore have been different. The types and forms of scales were established by Schlesinger in more than 25 years of research and published in 1938 in her book The Greek Aulos". Elsie Hamilton, one of her pupils, holds that "Miss Schlesinger was of opinion that the Modes came to birth long before even the time of Pythagoras [...] she points out that we can go back as far as 2800 B.C. to the silver pipes of Ur in Chaldea, which were excavated under the direction of Sir Leonard Woolley, and on which we find borings at equal distances and which, being made of silver have withstood the ravages of time [5]."
7.2.- An alternative way to study the monochord
There is a much simpler way to study sound frequencies using the monochord than to divide its string in a different number of segments each time. What if we divide it in a fixed number of parts and see what happens? We show in Figure 32 an example of the monochord divided into five equal segments. The whole string provides a reference frequency which is usually the tonic in modern musical theory, from which all other intervals arise in an ascending order (see Figure 31). However, the smallest segment in the divided string provides another reference frequency, actually the highest one for a given number of segments. Plucking an increasing number of segments every time generates the sound of lower and lower fractions of that highest frequency, which are known as undertones (Figure 32).
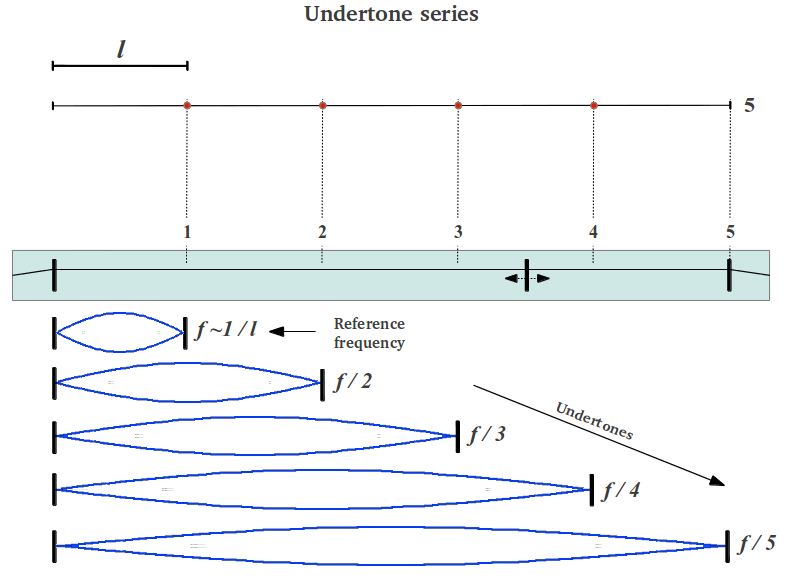 |
|
| Figure 32 |
Through this simple example we can start to appreciate the limitless possibilities of those undertones. The first overtone (f/2) forms with the reference (highest) frequency f the interval of an octave, although in a descending direction. Picking three segments we get the next overtone, which forms an interval of a descending perfect fifth with the second one as (f/3)/(f/2) = 2/3. Next we find another octave at f/4. The fourth undertone f/5 allows us to study the interval of a sixth (5/3) with the second one, and that of a major third (5/4). The following octave is not found until frequency f/8, thus the successive octaves contain an increasing number of (densely packed) intervals.
Next diagram by Elsie Hamilton illustrates this fact up to 16 segments. Please observe the following: (1) each segment's length is not proportional to the corresponfing interval in cents as in our colour drawings; (2) the fractions shown correspond to divisions of the string length -not to frequencies; and (3) the segment number increases from right to left. It is interesting to notice from this diagram that the first three octaves (up to the eigth undertone) contain most intervals of the Just scale, as explained in Figure 32 above in the reverse direction. To be able to play any such intervals, we would need a monochord with at least two strings. If that was the case, holding one string for example at the fifth segment and the other string at the third segment and playing them would produce the sound of a (descending) major sixth (3/5).
 |
|
| Figure 33: Division of a monochord into 16 equal segments illustrated by Elsie Hamilton [5]. The numbers shown are fractions of string length, the corresponding frequencies would be their inverse values. Playing an increasing number of segments provides a sequence of undertones 16/2, 16/3, 16/4, ... of the highest reference frequency 16/1 also called arché, until the lowest frequency 16/16 is reached at the whole string length. |
The ancient Greek Aulos Modes start in next octave, the one contained between the 8th and the 16th undertones. Following Maria Renold's method, I will show you how to easily derive the first one of those modes using exclusively the harmonic mean.
7.3- Derivation from the harmonic mean
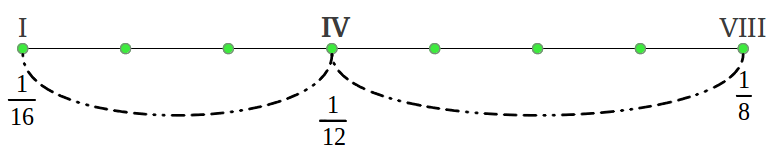
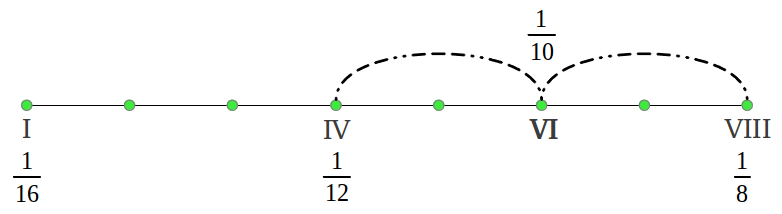
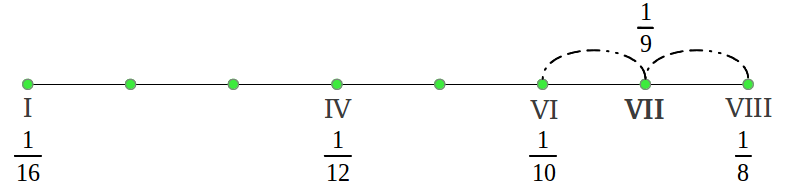
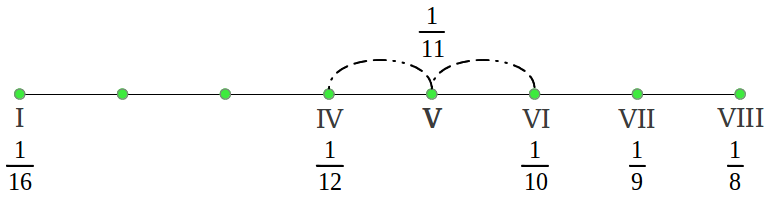
Lets pick the octave contained between the frequencies of the 16th undertone (f/16) and the eigth one (f/8) of some reference frequency or Arché f not to be confused with the tonic in the scale which in our case would be f/16. As we already know from Figure 24, the harmonic mean of the octave generates the fourth note (actually a perfect fourth). Now if we continue with harmonic means instead of switching to the arithmetic mean, we obtain the frequency of the six remaining notes as follows:
|
(a) |
|
|
(b) |
|
|
(c) |
|
|
(d) |
|
|
(e) |
|
|
(f) |
|
|
(g) |
|
 |
|
| Figure 34: The structure of the scales in the ancient Greek Aulos Modes can be obtained exclusively from the harmonic mean. |
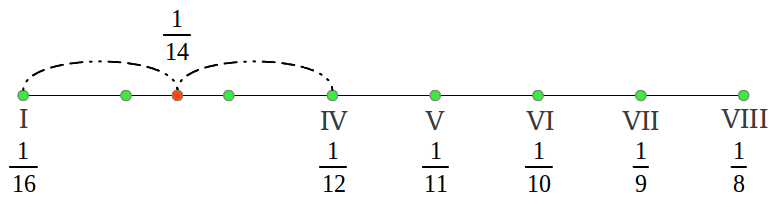
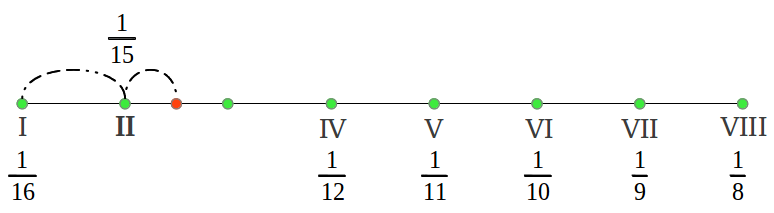
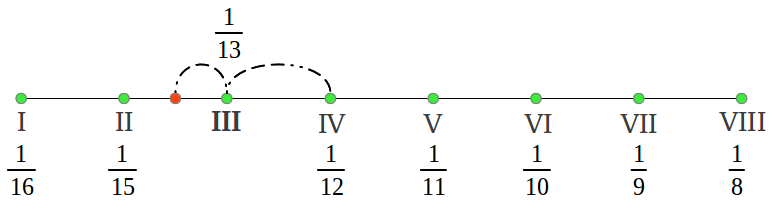
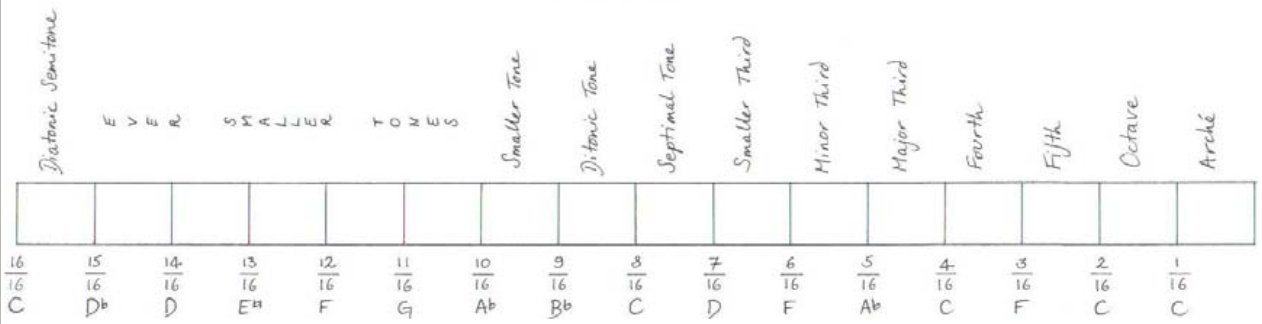
What we have obtained is what mathematicians call a harmonic series, except for the missing 1/14 which would be a 9th note in the scale. Those are the frequencies of the ancient Hypodorian Saturn Mode [2]. The notes in the Aulos Modes are usually numbered in terms of the segment number that produces each note [2]. Figure 35 shows the actual interval lengths in cents following that numbering and using our colour convention (see the colour legend in Figure 38). We can see that the first interval is (1/15)/(1/16) = 16/15 or a chromatic semitone, the following four intervals 15/13, 13/12, 12/11 and 11/10 are "new" to us and characteristic of the Greek Modes, and the last two intervals also sound familiar: 10/9 the just wholetone and 9/8 the "pythagorean" wholetone.
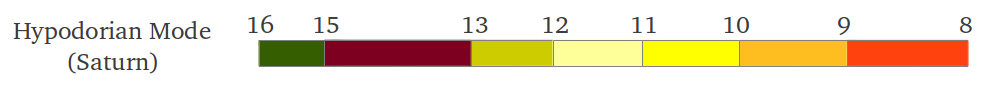 |
|
| Figure 35 |
In order to play this scale in a monochord, we would have to divide it in 16 equal segments as in Figure 33 above and use only the second half of the divisions. Please note that, despite being based on the undertone series, when read from left to right the Hypodorian Saturn Mode is actually an ascending scale.
7.4.- The seven ancient Greek Modes
The remaining six Greek Modes are obtained using 18, 20, 22, 24 and 28 string divisions, as illustrated in the following original diagram by Elsie Hamilton [5]:
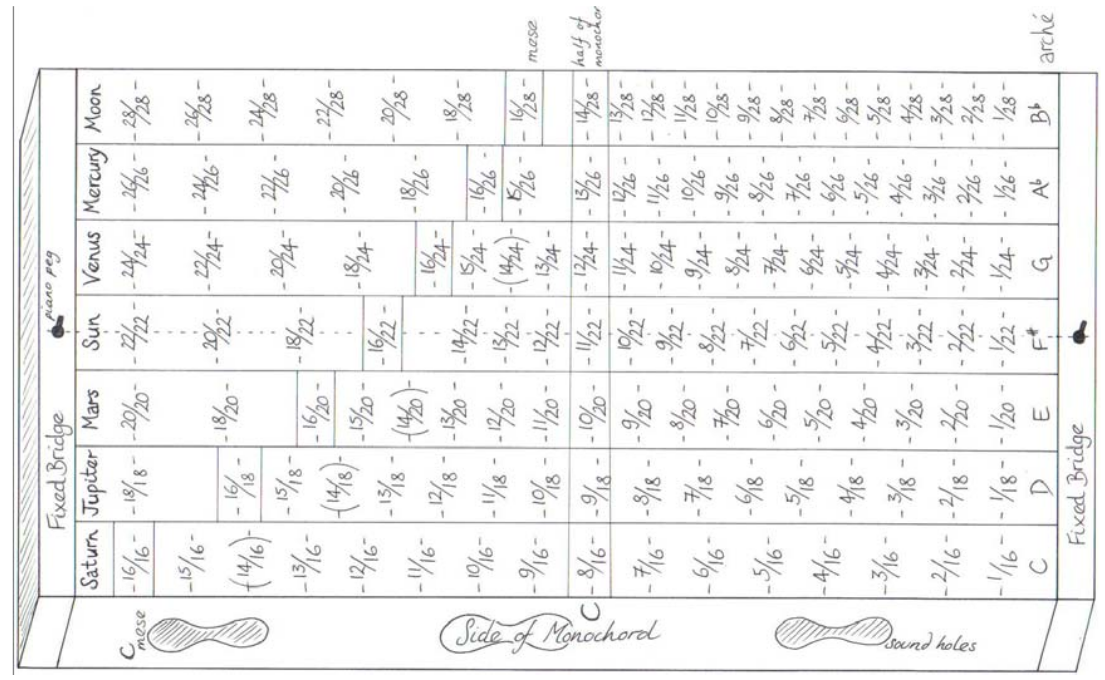 |
|
| Figure 36: Divisions in a monochord to play the seven Greek Aulos Modes. |
We can observe in this diagram that each mode has a different basic segment length, for the whole string length is the same. Therefore, the reference frequency or Arché is different for each mode. For example if we adjust the whole string length L so that its fundamental is f0 ~1/L = 128Hz, then the Arché of the Saturn mode would be f=128/(1/16) = 128·16 = 2048 Hz, but the Sun mode would have an Arché f = 128·22 = 2816 Hz. Please notice that the notes that lie below (to the left of) the 16th undertone use the doubled undertones of the diatonic octave (8th to 16th) omitting the undertones that lie in between: for example the four lowest undertones of the Sun mode are 1/22, 1/20, 1/18, 1/16. The above diagram may be misleading because the length of the first segment, the one located between the first division and the beginning of the string, seems the same in every mode, but that is not be the case as we have just explained.
Now comes the interesting part. What about the interval structure of the six new modes that we have just obtained? If you conduct the mathematical calculations, you will end up noticing that all the modes contain the same intervals but in a different order. This is graphically illustrated in Figure 37. The center Sun Dorian mode was the principal mode in the old Greek musical system. Note that this mode has two forms, one using the 1/14 division and the other using the 1/15 division; not all the modes had those two forms (see Figure 40) but those two divisions were never used simultaneously in a mode.
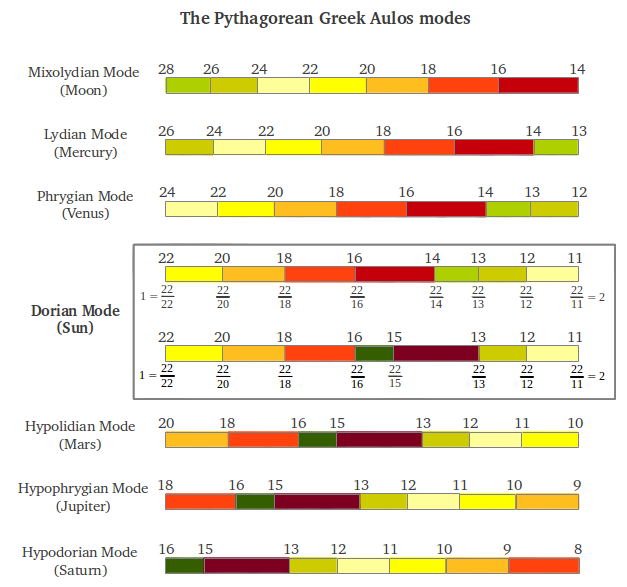 |
|
| Figure 37 |
The seven ancient Greek Modes have a characteristic feature: each one of them is formed by two different tetrachords. This is illustrated in the following figure, where we show each interval length in cents. We can appreciate that each mode can be generated from the previous one by picking the last interval and inserting it in the beginning, doing a cyclical shift (except in the cases where the 15/13 interval is replaced by the 15/14 interval or conversely, Figure 38).
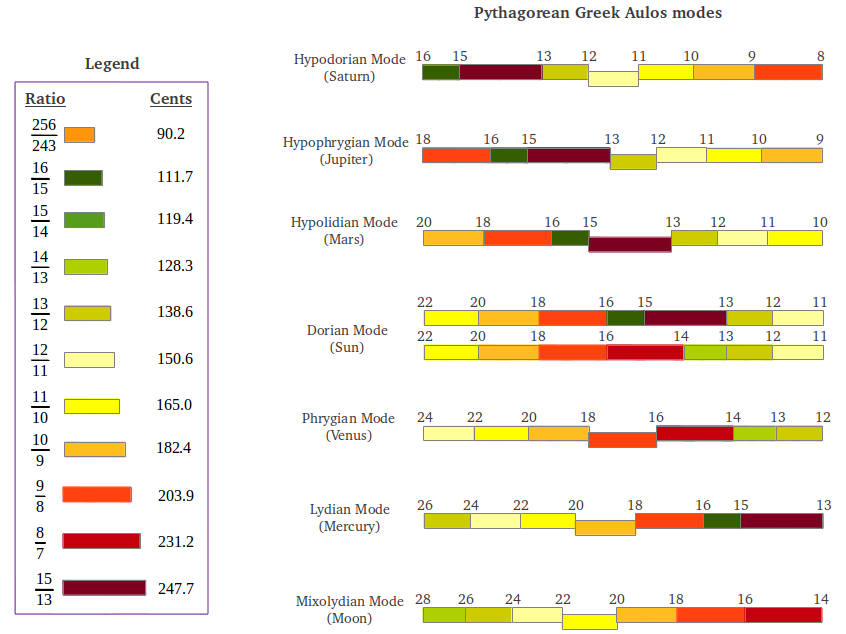 |
|
| Figure 38: The ancient Greek Aulos Modes as tetrachords. |
Does any of the above tetrachords sound familiar to you? As you may have guessed, it is the first tetrachord of the Hypolidian Mars Mode. The modern Just Intervals scale uses this tetrachord actually twice, following the typical Aristoxenus arrangement (Figure 39). It appears that the modern diatonic scale has lost the original purity or diversity of intervals that it use to have in the ancient Hypolidian Mode.
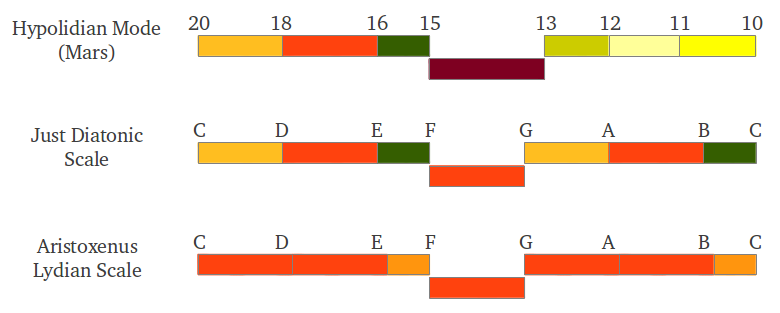 |
|
| Figure 39: Our modern Just Intervals scale contains the first tetrachord of the Hypolidian Mars Mode. |
7.5.- The Greek Aulos Modes as subspecies
In order to play the seven different modes in a single instrument, it would have to be retuned each time because the number of string divisions is different in each mode. However, there is a way of overcoming this apparent drawback. The trick is to divide the string into a sufficiently high number of divisions (at least 28), and to "accomodate" each mode in a different portion of the string. With this operation, all seven modes share the same middle interval 18/16 (called mese by the ancient Greeks) and also the same reference frequency, but each mode has its own tonic and, as surprising as it may seem at first, their interval structure is preserved! The following figure illustrates this fact, graphically reproducing Table 5 of Maria Renold's book [2, p.30].
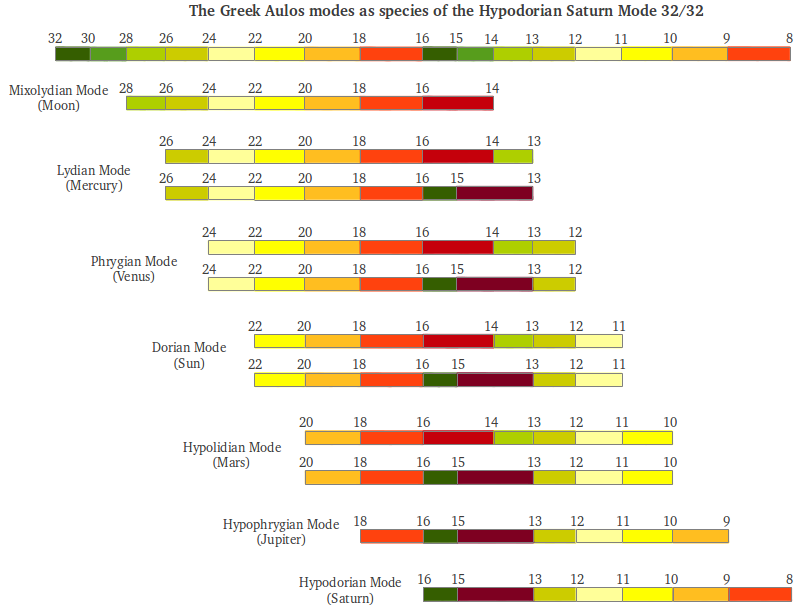 |
|
| Figure 40: The ancient Greek Aulos Modes as species. |
According to Elsie Hamilton, who has adopted the Greek Modes as a basis for musical composition, "with the seven Planetary Modes we have not only two different experiences as in modern Major and Minor scales, but at least seven, because each of the Greek Modes give us an entirely different "ethos" or atmosphere, which is quite individual and peculiar of that mode only, so that our musical experience is enormously increased thereby." According to her, another advantage is that "the Greek Modes are built on Nature's law itself (the Harmonic Series) without any compromise [as it happened in the spiral of fifths in Aristoxenus' scale], and a piano tuner finds it far easier to tune a piano to the Modes than in the ordinary way, with its complication of beats and so on" [5].
8.- The Scale of Twelve Fifths
8.1.- The scale structure and the formed fifths
Back in 1962, departing from the "Pythagorean" C scale presented in section 2, Maria Renold aurally found a twelve-tone chromatic scale in which free passage through all major and minor keys is possible, and which is made up entirely of what she calls aurally genuine intervals. These scale was called the scale of twelve fifths [2]. The structure of the scale is very simple: starting from the seven note "Pythagorean" C scale, a new tone is inserted in the middle of each wholetone which is the geometric mean of the two extreme frequencies of the corresponding wholetone (Figure 41). This is equivalent to placing the five extra semitones -which correspond to the black keys of the piano- in the exact middle of the wholetone in cents. Figure 41 shows the cumulative interval ratios of the resulting the twelve-tone chromatic scale obtained by this method. The length of the resulting intervals in cents are compared with those in the scales discussed so far in Table 2. In order to make clear that the five new tones are true geometric mean tones and to differenciate them from ordinary and equal-tempered tones, they are called Delis, Elis, Gelis, Alis and Belis -in the German language Ges means flat and Gis means sharp, so Gelis contains both names and it indicates that they are neither sharp nor flat semitones [2, p.8].
 |
|
| Figure 41 |
 |
|
| Table 2 |
It is important to stress that the five geometric mean tones were found by ear. The qualities of these new intervals differ from the intervals in the Just and Aristoxenus scales, so Maria Renold calles them "formed" intervals. According to her, "these formd intervals harmonize with the true intervals to make well-sounding harmonies and characteristic dissonances". The twelve tones form "a genueine sounding chromatic scale and 24 equally genuine sounding major and minor scales that are suitable for the realization of all works of music on instruments of fixed tuning. A trial with any instrument tuned in this way will show this to be the case, making the unsatisfying, false-sounding equal-tempered tuning unnecessary" [2, p.57].
Pianos can be tuned to the scale of twelve fifths. Listeners commented that the sound of Maria Renold's newly tuned piano did not appear to come directly from the instrument itself "but sounded freely as if they proceeded from the center of the room. A similarly free-sounding tone was observed with a choir of about 20 lyres tuned in this way; players and listeners experienced an inspiring fullness of sound that came from the middle of the room [...] Previously it appeared that only specially gifted artists, instrumentalists and conductors were able to create this free tone in active music making. The scale of twelve fifths appears to birng this free tone into existence simply by means of the interval proportions of the tuned tones" [2, p.63].
Maria Renold also stresses the fact that her scale of twelve fifths "only became possible after the discovery of what she called the formed fifth. That an aurally genuine fifth exists which is smaller than the tempered fifth is a phenomenon that can only be discovered by ear. The formed fifth is recognizable by its somewhat raw or dry character. It differs from all other fifths that have been acoustically classified until now" [2, p.61]. The following figure illustrates the twelve fifths in this scale; ten of them are perfect fifths and two of them are formed fifths -they contain two "Pythagorean" semitones instead of one:
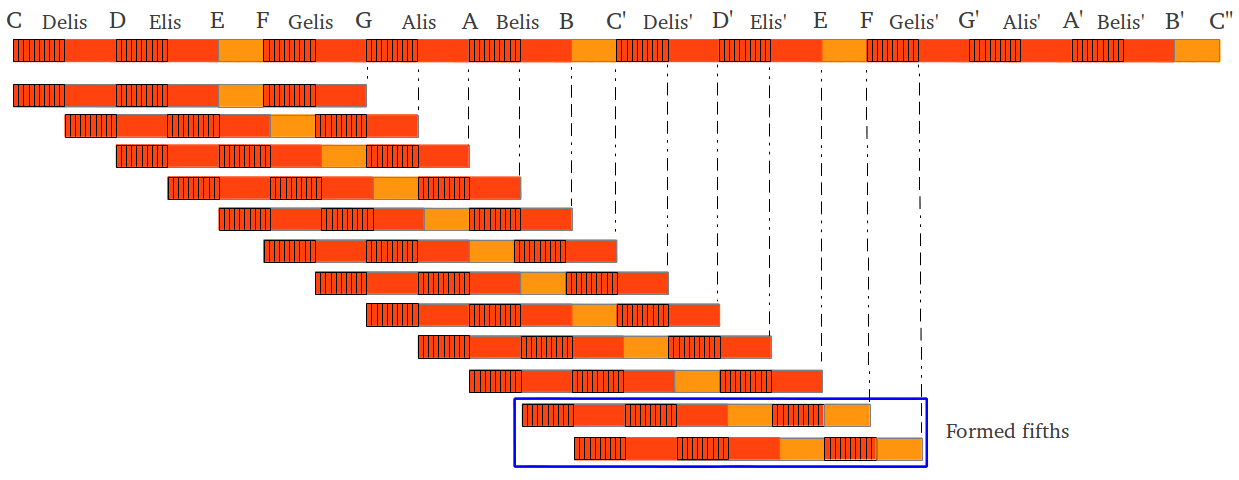 |
|
| Figure 42: The fifths in Maria Renold's scale of twelve fifths. |
8.2.- On the right concert pitch A=432Hz
Maria Renold also stresses that "a reference must be made to a key characteristic of the scale of twelve fifths. Just as the intervals and tones have a beautiful, pleasant and harmonic effect on the human being when tuned to C=256Hz, Gelis=362.04Hz and A=432Hz, so they become antisocial, and indeed cause people to provoke one another if the concert pitch A=440Hz [of common use today] is used. This frequently made observation shows that aurally genuine intervals are not of sole importance in music, but that tones of certain frequencies have characteristic qualities that can have major effects on human beings" [2, p.63]. This comment arose from the following experiences:
"The first time Maria Renold (concert violist and violinist) tuned her Steinway grand piano to the newly found tuning, the only tuning fork she had was A=440Hz, and the piano was therefore tuned according to this pitch. Once this was done, it was an occasion to celebrate and music was inmediately payed on the instrument with its absolutely wonderful sound. Classical and modern works sounded in a beauty not heard before, but after a while an increasingly spiteful atmosphere developed amongst the people present".
"It seemed totally improbable that the perfectly clear and harmonic sounding intervals of the new tuning method should arose such an antisocial mood amongst the listeners. However, it did arise. The solution was only found when the piano was retuned to Rudolf Steiner's suggested pitch of C=256Hz, the 'philosopher's C'. When more music was played on the retuned piano, it truly was a celebration. The spitefulness experienced earlier had gone and both intervals and tones sounded pleasant and beautiful. Everyone present was delighted at the splendid sound and felt sustained by a harmonic mood that left people free".
"To make sure that the first, for musicians' unusual observation, was not a deception, the experiment was repeated with lyres over many years and in many places. The same phenomena always took place. The observation can lead to only one conclusion: it can only be the tones based on A=440Hz that cause the antisocial mood" [2, p.69].
The the following question arises naturally ¿is that observation also valid for the remaining scales such as the widely spread Equal Temperament? In the following article we shall describe the experiments conducted by Maria renold to confirm than that is indeed the case.
9.- References
[1] Sethares, William A: "Tuning, Timbre, Spectrum, Scale", Springer, 2004.
[2] Renold, Maria: "Intervals, Scales, Tones and the Concert Pitch c = 128 Hz", Temple Lodge, 2004.
[3] Simpson, Peter LP: "The sound of Music: On the Ancient Greek Modes".
[4] Kappraff, Jay: "Beyond Measure, A Guided Tour Through Nature, Myth, and Number", World Scientific, 2002.
[5] Hamilton, Elsie: "The Modes of Ancient Greece", 1953.