- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Phi y Música en el ADN
1. Introducción
Como sucede a menudo en la investigación, los resultados que se presentan en este artículo se hallaron "accidentalmente" mientras estaba tratando de replicar los resultados de Jean-Claude Perez sobre las poblaciones acumuladas de los codones del ADN [1]. Este investigador ha estado estudiando durante años las poblaciones de codones del genoma humano completo (no sólo el 2% de ADN codificador). Calculando los cocientes de las poblaciones de codones acumuladas de distintas formas, obtuvo el atractor (3-φ)/2 relacionado con la Razón Aurea. Con una metodología similar, he descubierto dos resultados sorprendentes:
- Las poblaciones relativas de diversos grupos de ocho codones del ADN humano corresponden a ratios de notas musicales.
- Las poblaciones relativas de unos grupos específicos de ocho codones del genoma humano completo corresponden a exacamente la Razón Aurea φ.
2.- Conceptos Básicos sobre el ADN
Nuestra información genética está codificada en el ADN en forma de textos formados por "palabras" de 3 "letras". Estas palabras se llaman codones. cada letra de un codón proviene de 4 posibles bases nitrogenadas: A (adenina), C (citosina), G (guanina) y T (timina). El sistema de codificación es similar en todos los organismos vivientes y se conoce como Código Genético. Hay 43=64 combinaciones posibles (palabras) de estas 4 bases (grupos de 3 con posibles repeticiones). Habitualmente se organizan de acuerdo a 4 columnas del conocido Mapa del Código Genético Universal (columna T, luego columna C, luego columna A, luego columna G) (Tabla 1).
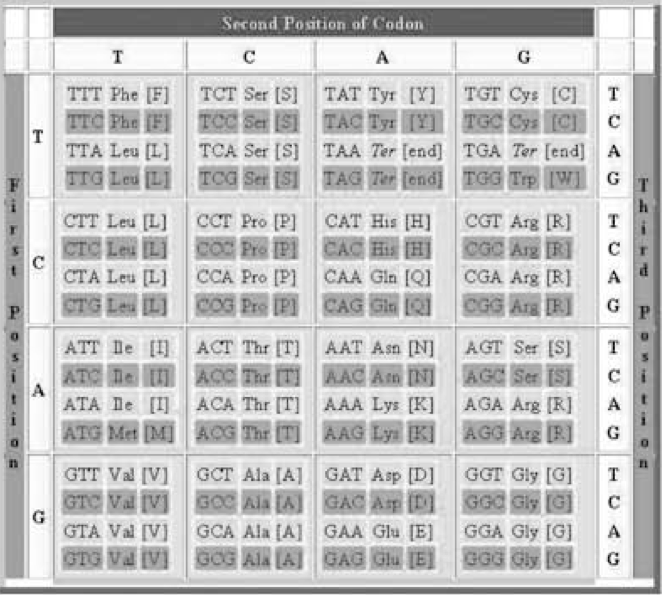 |
| Tabla 1: Los 64 codones del ADN dispuestos según el Mapa del Código Genético Universal. cada codón codifica un aminoácido (reproducido de [3]). |
Los 64 codones codifican los 22 aminoácidos conocidos, 20 de los cuales se encuentran en los humanos. Por lo tanto, algunos aminoácidos están codificados simultáneamente por diversos codones (ver Tabla 1). Este hecho se conoce como degeneración del código. Los aminoácidos són los constituyentes básicos de las proteinas, los componentes principales de cualquier organismo vivo.
Todas las funciones conocidas del control genético de un organismo están localizadas en aproximadamente el 2% del ADN, el llamado ADN codificador. El 98% restante se llama "ADN basura" porque se supuestamente no codifica nada. Las investigaciones que presentamos a continuación se han llevado a cabo utilizando todo el ADN.
La famosa doble hélice de la molécula de ADN tiene dos tiras relacionadas que contienen una secuencia de bases nitrogenadas. Estas tiras son complementarias: enfrente de una base A (o G) en una tira, siempre hay una base T (o C) en la tira opuesta.
3.- Metodología
En su trabajo Jean-Claude Perez analizó la totalidad del genoma humano (no sólo el 2% codificador) de la versión final “BUILD34” de 2003 [2]. Él consideró sólo una tira de la secuencia del ADN. Dada una secuencia de bases, por ejemplo TCAATGTCA, si el punto de inicio se desconoce existen tres formas posibles de agrupar estas bases en codones; en el ejemplo anterior estas tres lecturas posibles serían
1) TCA|ATG|TCA
2) CAA|TGT|CAT
3) AAT|GTC|ATC
Usando una tira completa del ADN, Jean-Claude Perez calculó, para cada una de las 3 posibles lecturas, el número total de cada uno de los 64 codones del código genético. En su libro "Codex Biogenesis" [3] también proporciona las poblaciones totales de codones obtenidas usando las 12 combinaciones posibles: (2 tiras x 2 sentidos por tira x 3 lecturas por sentido). Mis resultados se han obtenido al tratar replicar sus resultados en esta población de codones mayor (Tabla 2).
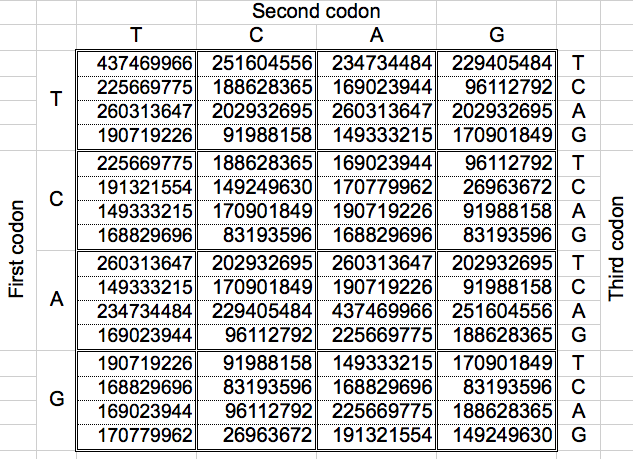 |
| Tabla 2: Las poblaciones acumuladas de las 12 posible combinaciones de lectura de los 64 codones del ADN, organizados según el mapa del Código Genético Universal (Total: 11373646448) [3]. |
Partiendo de esta tabla, empecé sumando las poblaciones de codones en los grupos sugeridos por Jean Claude Perez según los pliegues de papel de la curva Dragón (Figura 1) [1]. Esto me llevó a replicar algunos de sus resultados en [1] (sección 4). DEspués de esto, decidí investigar los cocientes de poblaciones acumuladas de grupos de 8 codones. Esta operación puede hacerse horizontalmente o verticalmente pero los resultados finales son casi los mismos (sección 5). Estaba buscando atractores relacionados con la Razón Aurea, y los encontré calculando los cocientes de poblaciones acumuladas de codones en unos grupos específicos de ocho codones alternados (Sección 6).
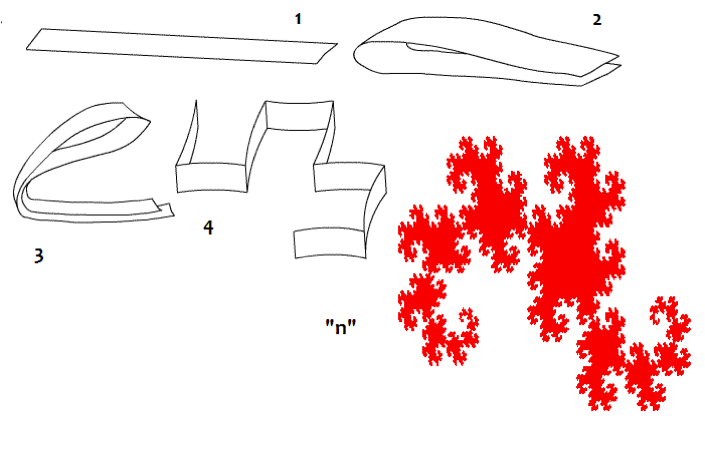 |
| Figura 1: Doblando un papel según la curva Dragón. |
4.- Replicando los resultados de Jean-Claude Perez
La curva Dragón incluye un mecanismo de pliegues muy común en la teoría del caos de Poincare (Figura 1). La matriz de la población de codones (Tabla 2) se particionó siguiendo los seis primeros pliegues de la curva Dragón:
Dragon 1: 2 particiones of 32 codones
Dragon 2: 4 particiones of 16 codones
Dragon 3: 8 particiones of 8 codones
Dragon 4: 16 particiones of 4 codones
Dragon 5: 32 particiones of 2 codones
Dragon 6: 64 particiones of 1 codones
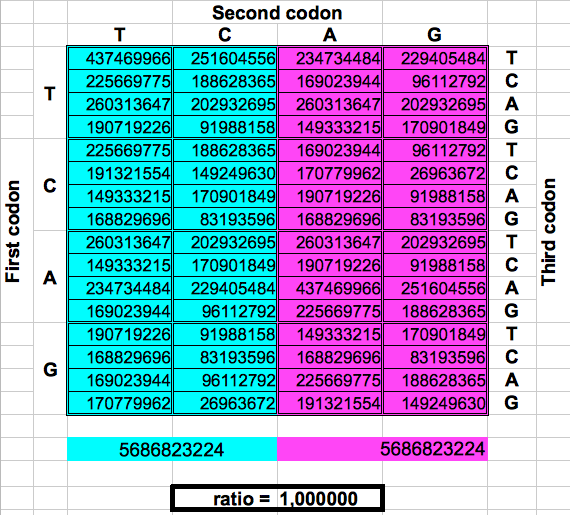
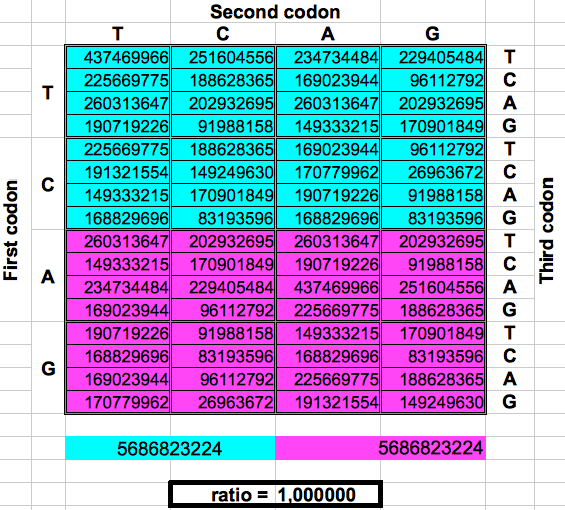
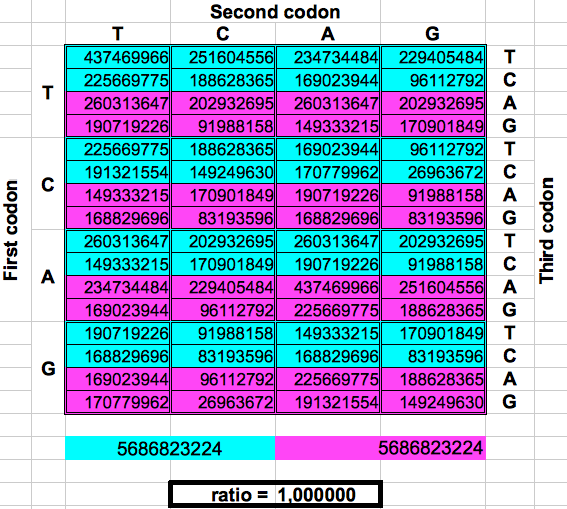
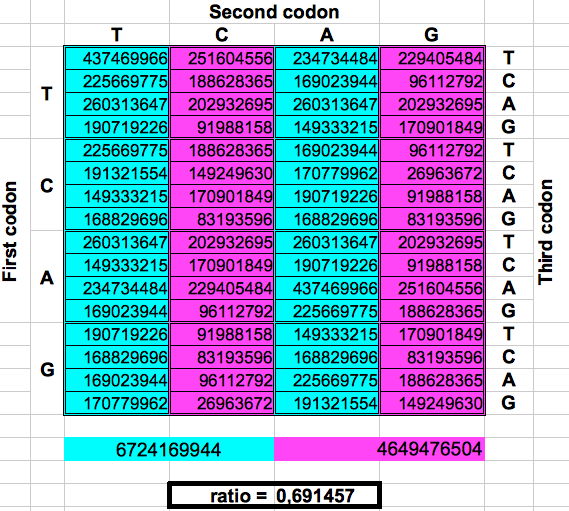
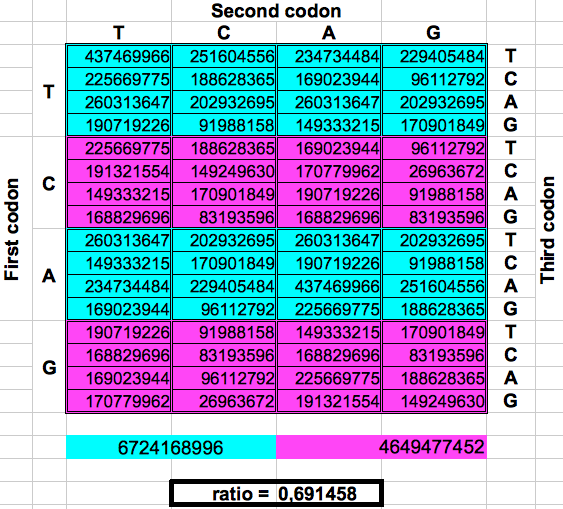
La figura siguiente muestra de forma gráfica estos dobles o particiones. Para cada una, el número total de codones en la región lila se dividió por el número total de codones en la región azul. El resultado fueron los dos valores préviamente reportados por Jean Claude Perez: cociente lila/azul=1 en los pliegues 1, 3 y 5. y cociente lila/azul=(3-φ)2 en los pliegues 2, 4 y 6. El atractor 1 corresponde a los ratios de bandas A o G respecto a las bandas T o C, mientras que el atractor (3-φ)/2 corresponde a los ratios de bandas C o G respecto a las bandas T o A.
| DRAGON 1 | DRAGON 3 | DRAGON 5 |
 |
 |
 |
| DRAGON 2 | DRAGON 4 | DRAGON 6 |
 |
 |
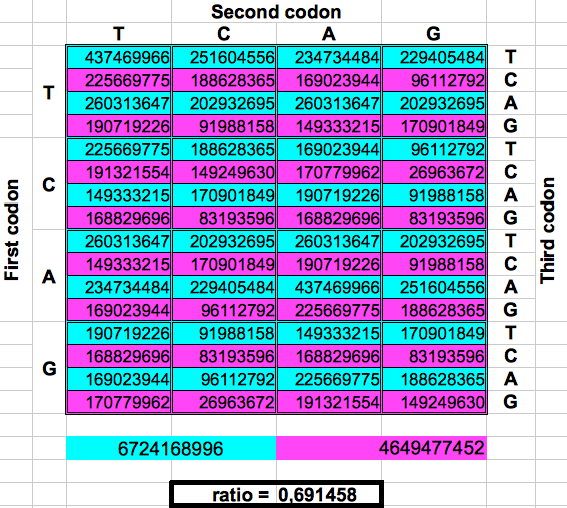 |
| Figura 2: Particiones de la población de codones en el genoma humano completo siguiendo los pliegues de la curva Dragón. | ||
Mis resultados están resumidos en la Tabla 3. El error entre el valor experimental y teórico del atractor (3-φ)/2 es de sólo 0.069%. Esto muestra que lo resultados obtenidos por Jean Claude Perez usando las tres lecturas posibles de una sola tira de ADN siguen siendo válidos en una población más grande obtenida usando las 12 posibles combinaciones de lectura.
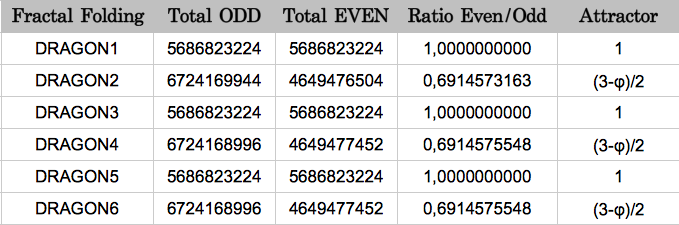 |
| Tabla 3 |
5.- Notas musicales en el ADN
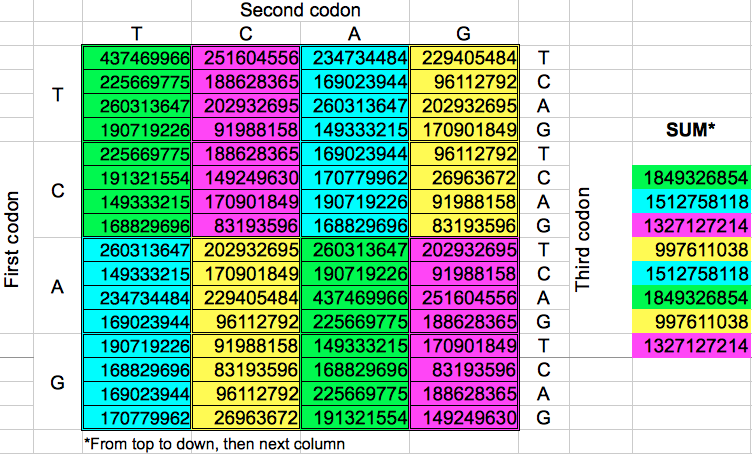
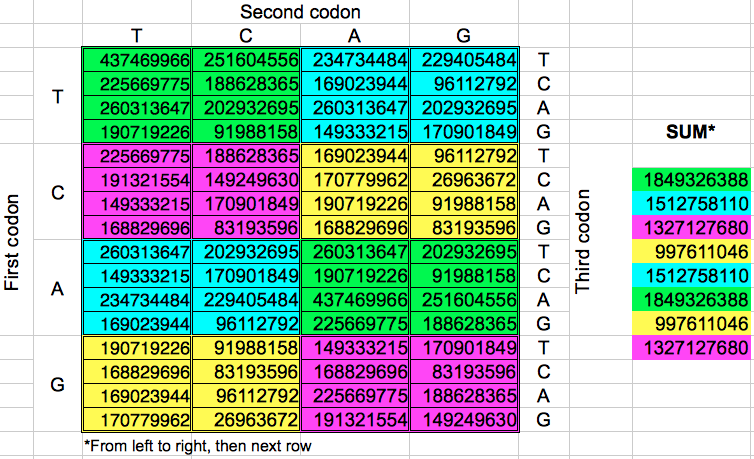
Partiendo de las poblaciones de codones de la Table 2, sumé las poblaciones en grupos de 8 codones consecutivos. A pesar de que hay ocho de esos grupos, obtuve sólo cuatro valores diferentes para la población acumulada (Tabla 4). Cuando esta operación se replica en la dirección opuesta, los resultados finales son prácticamente los mismos: cuatro valores acumulados muy parecidos a los anteriores. Un examen más detallado de cada grupo de ocho codones del mismo color revela que los codones correspondientes en cada grupo tienen las mismas poblaciones pero en un orden distinto.
 |
 |
|
| Tabla 4: Poblaciones acumuladas de grupos de ocho codones consecutivos seleccionados en horizontal o en vertical. | ||
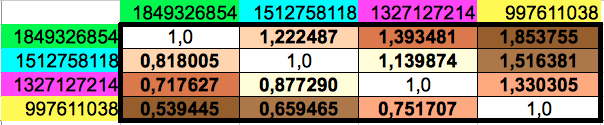
A continuación calculé los cocientes entre cada par de los cuatro valores acumulados, lo que conduce a la matriz de la Tabla 5. Se puede observar que la diagonal inferior de esta matriz contiene los valores inversos de los de la diagonal superior. Los resultados para la selección horizontal o vertical de los codones sólo difieren en el sexto decimal de cuatro de los doce valores no diagonales.
 |
 |
|
| (a) | (b) | |
| Tabla 5: Cocientes entre cada par de poblaciones acumuladas en grupos de 8 codones consecutivos. La diagonal inferior de esta matriz contiene los valores inversos de los de la diagonal superior. | ||
Con estos cálculos estaba buscando alguna relación de estos cocientes de poblaciones de grupos de codones con la Razón Aurea. En su lugar lo que encontré fué que los cociente resultantes estaban muy próximos a los ratio de las notas musicales en una octava. Para el lector sin conocimientos musicales como yo, repoduzco en la Tabla 6 las doce notas distintas de una octava siguiendo la escala de temperamento justo. Esta consiste en dividir la octava en 12 valores equiespaciados en el dominio logarítmico. Eso se traduce en la raiz doceava de 12 potencias consecutivas de 2 en el dominio lineal. Cada valor tiene una aproximación fraccional que también se muestra en la tabla.
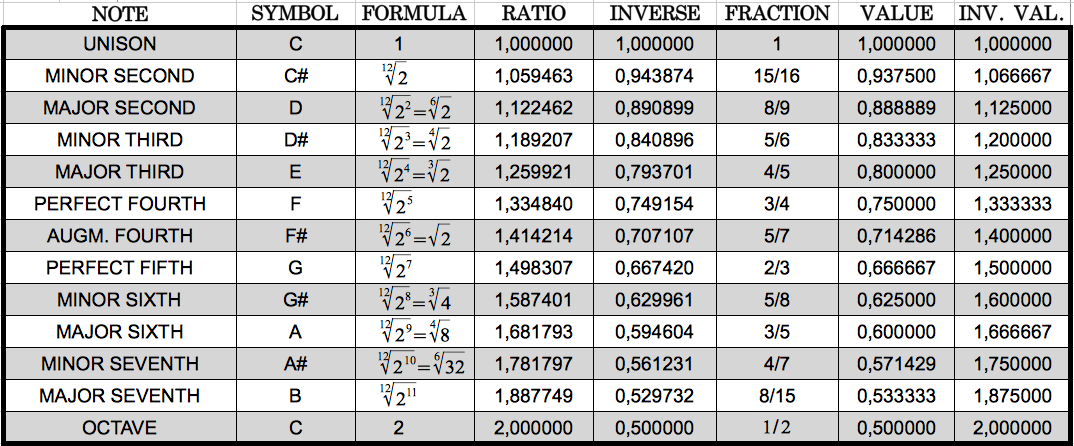 |
| Tabla 6: La escala de temperamento justo en una octava. |
La Tabla 6 me permitió darme cuenta que los cocientes que había obtenido correspondían muy de cerca con notas musicales. Estas notas están destacadas en colores en la tabla siguiende, usando los mismos colores que en la Tabla 5 anterior para facilitar la comparación.
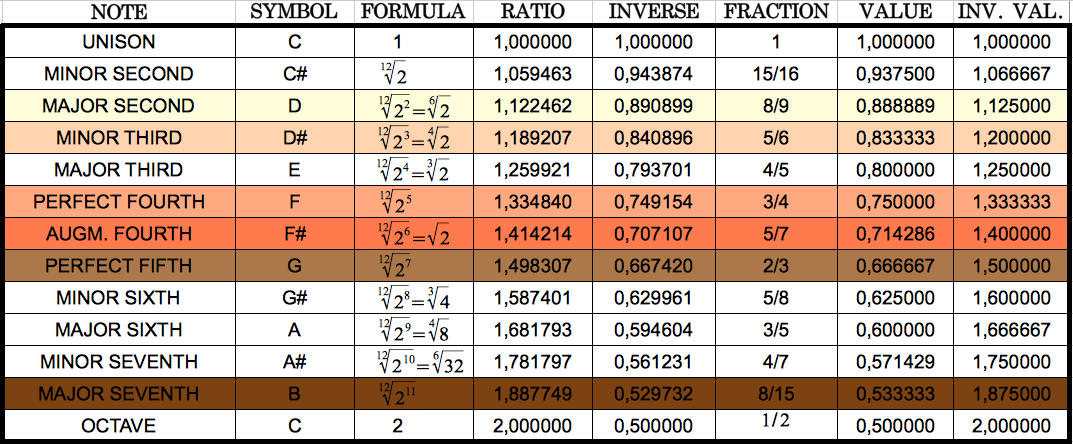 |
| Tabla 7: Las seis notas musicales que concuerdan con los seis cocientes de poblaciones de codones mostrados en la Tabla 5. Cada cociente y su correspondiente nota comparten el mismo color. |
En la tabla siguiente se muestran los errores absoluto y relativo entre cada cociente de población de codones y su nota musical correspondiente. Puede apreciarse que el error está siempre por debajo del 2.8% (0.033), con un promedio de 1,53% (0.021). En otras palabras, la precisión media es del 98.47%!!
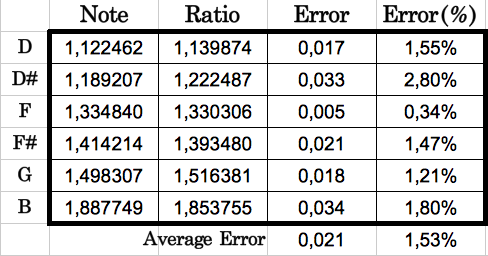 |
| Tabla 8: Comparación de cada cociente de población de codones con su nota musical correspondiente. El error promedio es tan sólo del 1.53% |
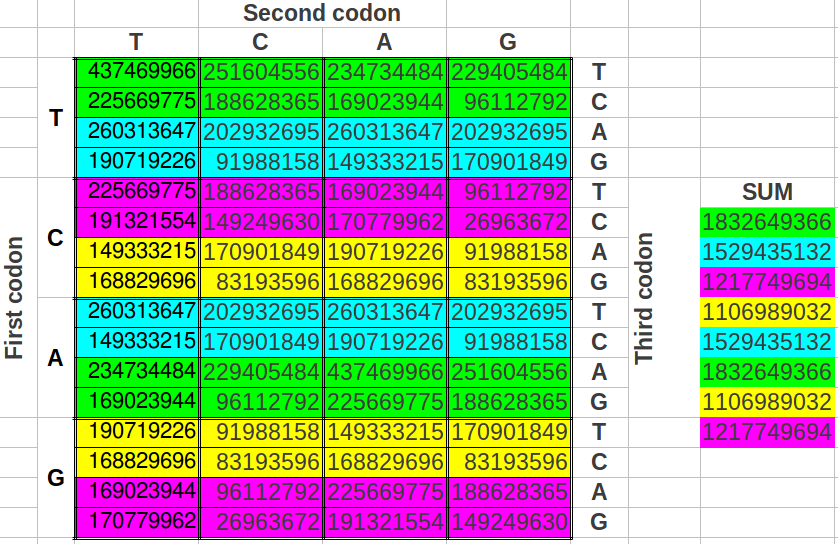
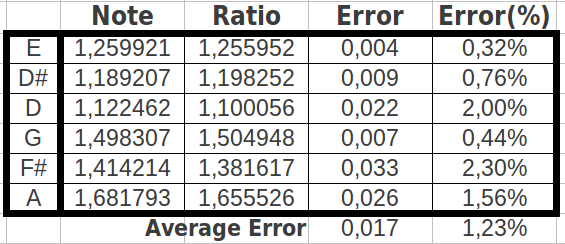
El lector familiarizado con la tabal del Código Genético Universal probablemente encontrará inusual la forma que hemos elegido para agrupar ocho codones consecutivos. Ello es así porque los codones se suelen numerar consecutivamente en la dirección horizontal, y de una fila se salta a la otra. ¿Cuál sería el resultado si agrupásemos los codones siguiendo esta forma más "natural"? Como cabría esperar, las poblaciones de codones también se acumulan en cuatro valores posibles (Tabla 9a) y lo cocientes posibles entre estos valores nuevamente se asemejan a notas musicales (Tabla 9b) con un error incluso menor que en los dos métodos de ordenación anteriores (0.017 o 1.23%, precisión 98.77%, Tabla 9c). Los resultados son también seis notas musicales, pero éstas son distintas que en los casos anteriores (Tabla 10).
 |
 |
|
| (b) | ||
 |
||
| (a) | (c) | |
| Tabla 9: Resultados obtenidos al seleccionar los grupos de ocho codones siguiendo el orden "natural" del mapa del Código Genético Universal. | ||
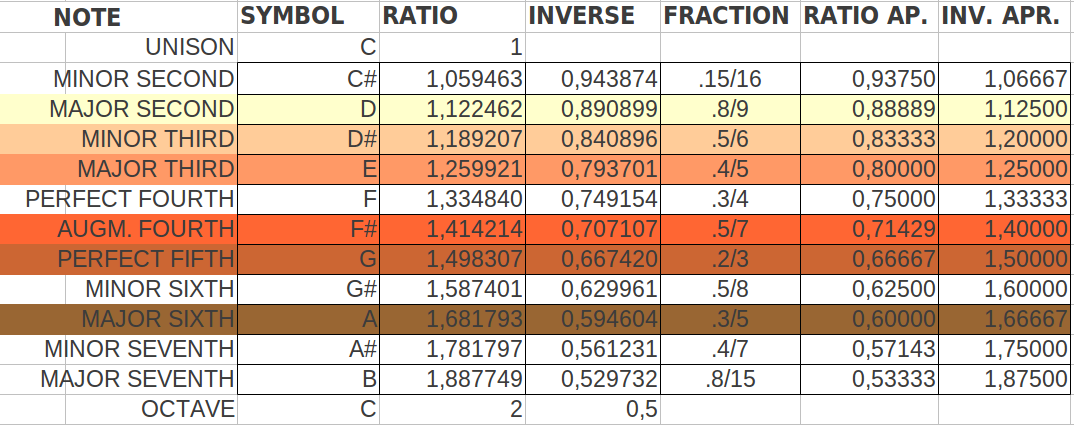 |
| Tabla 10: Las seis notas musicales que coinciden con los seis cocientes de poblaciones de codonesde la Tabla 9. Las notas resultantes son distintas que en los casos anteriores. |
6.- La Razón Aurea vuelve de nuevo
Hay muchas formas de hacer grupos de ocho codones en la tabla del Código Genético Universal. La pregunta siguiente me vino a la cabeza: ¿cuál sería el resultado si cogiéramos los grupos de ocho codones en subgrupos alternados de cuatro? Para mi sorpresa, los valores acumulados de esos grupos se redujeron a tan sólo tres en lugar de cuatro valores distintos (Tabla 11).
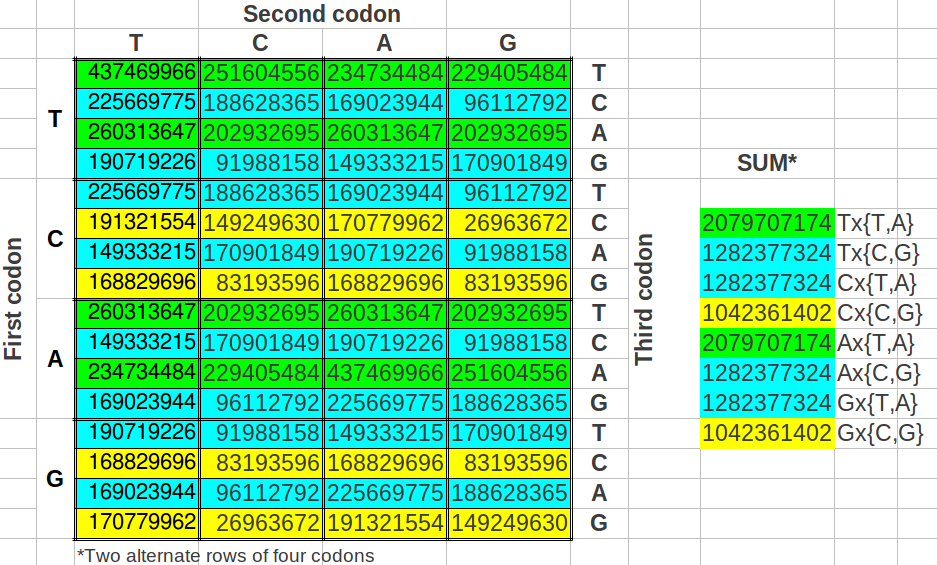 |
| Tabla 11: Poblaciones acumuladas de los grupos de ocho codones seleccionados en filas alternas. |
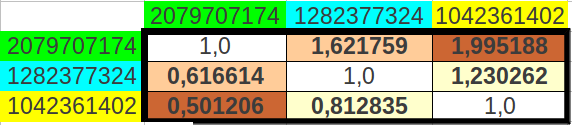
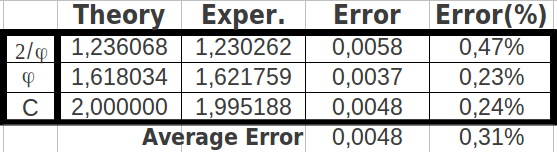
Y cuando calculé los cociente posibles entre estos tres valores, el resultado fué sorprendente: uno de los valores resultantes fue la mismísima Razón Aurea φ, otro valor fue una octava exacta (2), y el tercer valor fue el cociente entre estos dos (2/φ) (Tabla 12a). El error entre los valores exactos y experimentales es de tan sólo el 0.31% (Tabla 12b).
 |
 |
|
| (a) | (b) | |
| Tabla 12: Los cocientes de poblaciones acumuladas de grupos de ocho codones seleccionados de forma alternada corresponden a la Razón Aurea, a una octava perfecta, y al cociente entre ambas. | ||
7.- Discusión
En este artículo hemos podido confirmar que los resultados relacionados con la Razón Aurea obtenidos por Jean-Calude Perez en la población de codones de una sola tira del ADN siguen siendo válidos cuando se consideran las poblaciones de codones del ADN de dos tiras y los dos sentidos de lectura. El mecansimo de pliegues siguiendo la curva Dragón proporciona tres formas de particionar los codones del Genoma Humano completo en dos mitades con exactamente la misma población (propoción=1); ello pone de relieve la simetría y la redundancia inherentes al código genético humano. Pero el pliegue siguiendo la curva Dragón también proporciona otra tres formas de dividir los codones del genoma humano en dos mitades cuya población acumulada está en una proporción relacionada con la Razón Aurea que es (3-φ)/2. Ello muestra que, a una escala global, la Razón Aurea armoniza la población de codones completa. Nótese que esta armonía es válida para el genoma humano completo, no sólo para el 2% de ADN codificador.
Cuando descendemos a una escala menor, es decir haciendo grupos de ocho codones en lugar de 32, la música entra en juego. En este caso, hemos visto por lo menos tres formas de seleccionar grupos de ocho codones de forma que los cocientes entre sus poblaciones corresponden a notas musicales. La secuencia de notas depende de la forma en que se forman los grupos. La similitud con las notas musicales tiene una precisión promedio del 98.77%. Por lo tanto, ello nos lleva a concluir que el genoma humano entero parece estar organizado según la teoría musical, almenos en la escala de grupos de ocho codones. ¿Es eso posible desde una perpctiva de evolución natural? Cuesta de creer. ¿Sabe Diós tocar música? Podría ser. La gran investigación del compositor escocés Stuart Mitchell y colaboradores ha revelado que el ADN es una partitura musical cósmica operando tripletes a un ritmo de unos 3000 latidos por minuto [4]. El investigador Susumu Ohno [3] ha mostrado que las secuencias de bases codificadoras del ADN pueden traducirse en partituras musicales y viceversa. Ohno dice: "El principio de recurrencia repetitiva está en todos los aspectos de la vida en la Tierra. Por lo tanto, los genes individuales del genoma han sido duplicados y triplicados a menudo hasta el punto de la redundancia [...] Este principio incluso parece gobernar las manifestaciones del intelecto humano; la composiciones musicales también siguen este principio de recurrencia repetitiva. Así pues, las bases de secuencias codificadoras pueden transformarse en partituras musicales siguiendo un conjunto de reglas. Y al contrario, las partituras musicales se pueden traducir en secuencias de bases codificadoras".
Por último, hemos descubierto que cuando los grupos de ocho codones se seleccionan de una forma muy específica, las notas musicales convergen a tan sólo tres valores resonantes: una octava (2), la propia Razón Aurea (φ) y la relación entre ambas (2/φ). Ello muestra claramente que la Razón Aurea no sólo opera a escala global (1/2) como ha mostrado Jean-Claude Perez, sino tambien a escalas muy inferiores (1/8). Las poblaciones de codones en el ADN a diferentes escalas parecen estar gobernadas tanto por la Música como por la Geometría Sagrada. Pitágoras dijo: "Hay geometría en el zumbido de las cuerdas, hay música en la separación de las esferas".
Se podría argumentar que nuestros resultados son debidos en parte a la simetría inherente a la doble hélice del ADN. Jean-Claude Perez ya demostró que en el ADN de una sola tira la Razon Aurea entra en juego a escala 1/2. Yo he podido verificar, aunque los resultados no se muestran aquí, que la similitud con notas musicales y la Razón Aurea φ siguen apareciendo en el ADN de una tira también a escala 1/8. Cualquier persona interesada puede replicar estas investigaciones o llevarlas una paso más allá con los datos proporcionados en las referencias [1-3].
8.- Referencias
[1] Perez, Jean-Claude, "Codon Populations in Single-stranded Whole Human Genome DNA Are Fractal and Fine-tuned by the Golden Ratio 1.618", Interdiscip Sci Comput Life Sci (2010) 2: 228–240.
[2] http://hgdownload.cse.ucsc.edu/goldenPath/hg16/chromosomes/
[3] Perez, Jean-Claude, "Codex Biogenesis",
[4] Ohno, Susumu; Ohno, Midori: "The All Pervasive Principle of Repetitious Recurrence Governs Not Only Coding Sequence Construction But Also Human Endeavor in Musical Composition", lmmunogenetics, 24: 71-78, 1986.
