- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Sólidos Sagrados en el Núcleo Atómico
1.- Introducción
"Nuestra imagen del nucleo es tan diferente de la imagen aceptada (en realidad, no hay ninguna imagen aceptada) como para hacer imposible comparación alguna. El especialista en la materia reconoce de inmediato que si estamos en lo cierto, el edificio entero de la física atómica del siglo XX tiene que ser repensado, como había hecho el Dr. Moon. Él era capaz de realizar avances allí donde otros no podían, en parte porque tenía la maestría práctica en los experimentos cruciales sobre los que la estructura teórica se había construido. Él los había llevado a cabo. Pocos de sus colegas tenían la combinación de competencia y coraje para pensar de la misma forma.
Laurence Hetch [1]
Este artículo describe una porción minúscula de la investigación llevada a cabo por el eminente físico nuclear Dr. Robert J. Moon (1911-1989) [2], y también introduce algunas posibles variantes del mismo. Me tropecé con el modelo geométrico del núcleo atómico del Dr. Moon al poco de saber de una elegante reorganización de la tabla periódica de los elementos en una estructura tetraédrica, conocida como la Tabla Periódica Perfecta [3]. Ello me hizo plantearme la siguiente pregunta: si los elementos atómicos pueden organizarse de esta manera ¿podrían los propios electrones estar organizados geométricamente de una forma regular dentro del átomo? Estoy convencido de que existe una respuesta afirmativa a esta pregunta, una que llegará a nosotros a su debido tiempo. Lo que sí que existe, y nadie te lo cuenta en la escuela, es un modelo geométrico bonito y coherente de la ubicación de los protones en el núcleo atómico, que involucra los Sólidos Platónicos.
Hasta donde la ciencia moderna sabe, todo átomo de la materia está constituido por partículas cargadas positivamente -protones- y partículas neutrales -neutrones- que se sabe que están concetrados en el núcleo atómico, y por partículas con carga negativa -electrones- que se encuentran a su alrededor. Estoy firmemente convencido de que todas estas partículas trabajan unidas como un conjunto, pero la física actual separa el estudio del nucleo del estudio del espacio extranuclear. En el momento actual, no existe ningún modelo teórico capaz de describir en detalle la estructura del nucleo. Cada uno de los modelos nucleares existentes describe algunas de las observaciones experimentales conocidas, pero no existe un modelo definitivo que las explique todas. El modeo nuclear del Dr. Moon encaja con algunas periodicidades halladas en diversas propiedades de los elementos atómicos, y también explica por qué algunos elementos -como el uranio- pueden tomar parte en la fisión nuclear.
En el transcurso de mis investigaciones redescubrí algunas interpretaciones alternativas de dos teorías físicas ámpliamente aceptadas: el electromagnetismo y la mecánica cuántica. Me sorprendió averiguar que, bastante antes de que James Clerk Maxwell publicara su famoso tratado del electromagnetismo -el que se enseña a todos los ingenieros de telecomunicaciones- Alfred Weber ya había propuesto una expresión general de la fuerza electrodinámica entre partículas cargadas en movimiento. De hecho, todas las ecuaciones de Maxwell para el campo electromagnético se pueden deducir de la electrodinámica de Weber [4]. El hecho interesante para la presente discusión es que la teoría de Weber predice una distancia por debajo de la cual la fuerza entre dos partículas con carga del mismo signo cambia de la repulsión a la atracción [5]. Cuando se sustituyen las constantes modernas en su fórmula, se obtiene el radio clásico del electrón ¡¡a pesar de que Weber desarrolló su teoría mucho antes del descubrimiento experimental del átomo!! Así pues, según la teoría de Weber, los protones cargados positivamente dentro del nucleo, en lugar de repelerse, se atraen entre ellos.
¿Y por qué preocuparse por la mecánica cuántica? Su interpretación más ampliamente aceptada sostiene que uno sólo puede trabajar con probabilidades de encontrar una partícula atómica en una posición determinada dentro del átomo, y que no tiene ningún sentido hablar acerca de la posición exacta o de la trayectoria de, por ejemplo, un electrón. ¡Y no digamos ya la posibilidad de que el electrón o el protón tengan una estructura interna! Afortunadamente, existe una interpretación alternativa sólida según la cual plantearse ese tipo de cuestiones ya ha dejado de ser una completa locura. Como sucede con la electrodinámica de Weber, probablemente muchos físicos la desconocen. Estoy hablando del potencial cuántico de De Broglie-Bohm. El propio Dr. Moon mencionó en una de sus entrevistas [6] que Louis De Broglie y David Bohm habían trabajado juntos en la interpretación de la ecuación de Schrödinger a través del potencial cuántico -también conocida como la teoría de la onda piloto- hasta la muerte de De Broglie. Esta interpretación de la mecánica cuántica, presentada por Louis De Broglie en la conferencia Solvay de 1927 [7], no sólo predice de forma exacta todos los hallazgos experimentales como lo hace el enfoque convencional (y algunos otros que éste no explica como el experimento de la interferencia de electrones en la doble rejilla o el efecto Aaron-Bohm) sino que también demuestra que la interpretación probabilística de la mecánica cuántica es una consecuencia -y no una premisa necesaria- y que ¡¡tiene sentido hablar de las trayectorias y las posiciones de las partículas atómicas!!
2.- Sobre la estructura de la materia
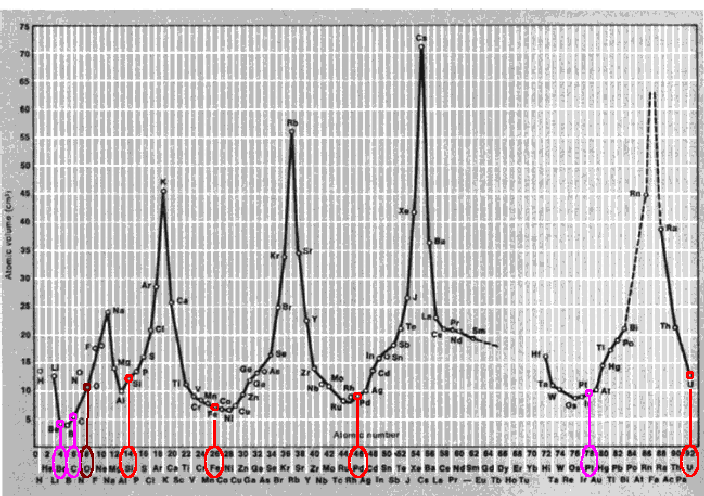
La figura siguiente muestra la Tabla Periódica de los elementos moderna. Cada elemento se caracteriza por su número atómico A, que cuenta el número de protones (partículas con carga positiva) en su nucleo. Este número también indica la cantidad de electrones (partículas con carga negativa) que rodean el nucleo cuando el elemento se encuentra en su estado estable, no ionizado. Cada elemento tambien se caracteriza por su número de masa Z, el cual tiene en cuenta el número N de neutrones (partículas neutrales) en el nucleo. Por lo tanto Z = A + N. Dependiendo del número de neutrones en su nucleo, algunos elementos tienen distintas variantes conocidas como isótopos, con el mismo número atómico pero distinto número de masa. Algunos isótopos no son estables y se desintegran rápidamente. De entre los isótopos estables de un elemento dado, la Tabla Periódica muestra la masa atómica del isótopo más abundante en la naturaleza. El número de masa generalmente puede obtenerse redondeanto la masa atómica al entero más cercano. Hablaremos sobre los elementos destacados en la tabla en la próxima sección.
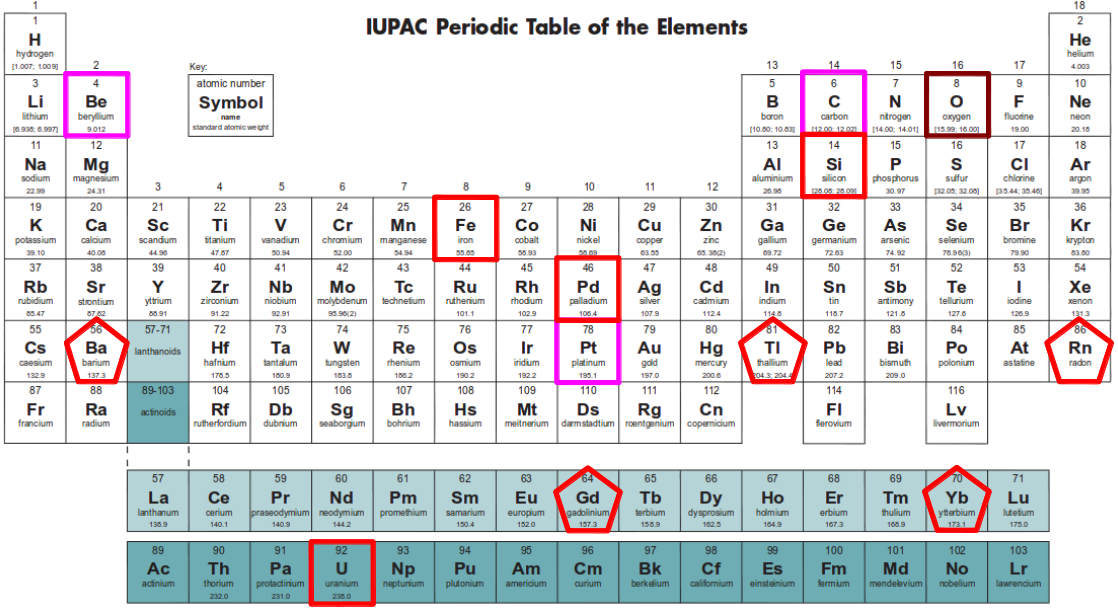
Figura 1: Tabla Periódica de los elementos (disponible aquí). Los elementos marcados con cuadrados rojos -ya sea rojo claro o rojo oscuro- indican que se ha completado una capa del primer conjunto de cuatro capas segun el modelo de Moon del nucleo. Los cuadrados magenta indican los elementos que yo propongo podrían indicar el cierre de capas adicionales no consideradas originalmente por Moon. Los pentágonos sobre determinados elementos indican que se ha completado una capa en la estrucutra dodecaédrica gemela del modelo nuclear de Moon.
¿Qué podemos decir acerca de la estructura interna de cualquiera de esas partículas? Por ejemplo, ¿qué es un electrón? La mayoría de físicos están de acuerdo en que se trata de una entidad que posee la propiedad de un cuanto de carga, y que no podemos inferir nada acerca de su composición interna a partir de los experimentos: sólo se nos permite hablar de la probabilidad de encontrar el electrón en algun lugar alrededor del nucleo. Afortunadamente, como he mencionado en la introducción, según la interpretación alternativa de la mecánica cuántica sugerida originalmente por Louis de Broglie en 1927, sí tiene sentido pensar en partículas cuánticas como entidades con estructura interna que se pueden mover en determinadas trayectorias -tal vez desconocidas [8]. Con respecto a la estructura interna de un electrón, según las investigaciones llevadas a cabo por el biofísico Dr. Paulo Correa y su mujer, éste consiste en un cuanto de energía circularizada en constante flujo definiendo una estructura toroidal [9]. El Dr. Vladimir B. Ginzburg también ha desarrollado un modelo sencillo en forma de toroide con relación de aspecto variable aplicable a todas las partículas elementales con carga [10].
¿Y qué sabemos acerca de la composición interna de un protón o de un neutrón? Los físicos no tienen una forma de mirar dentro de una cualquiera de esas partículas. Pero a partir de los experimentos en aceleradores de partículas están de acuerdo en que un protón (o un neutrón) está compuesto por tres unidades más elementales conocidas como quarks. Así pues en el dominio de la física nuclear ¡parece tener sentido hablar de la estructura de una partícula ja ja ja! De hecho algunos experimentos llevados a cabo en el Weizmann Institute of Science han demostrado que la corriente eléctrica está cuantificada en unidades de 1/3 del cuanto de carga [11]. Luego resulta probable que el electrón también esté compuesto por tres unidades elementales, pero por el momento la ciencia (aún) no sabe si eso es del todo cierto. Sospecho que tanto el protón como el electrón tienen una estructura interna común, y sólo difieren en tamaño y en su propiedad interna de carga. Podría muy bien tratarse de versiones escaladas el uno del otro. De hecho, los físicos mantienen que las partículas beta son electrones emitidos por el nucleo en el proceso de descomposición de un neutrón en un elemento radioactivo. De forma similar, un neutrón puede verse como un protón que se ha "fusionado" con un electrón. Pero por supuesto en ambos casos el tamaño de un tal electrón nuclear tiene que ser comparable al de un protón. Por lo tanto, todo parece apuntar a que los electrones del nucleo son versiones escaladas de sus compatriotas extra nucleares! Pero vamos a focalizarnos en el objeto principal del artículo.
3.- Algunas propiedades de los elementos atómicos
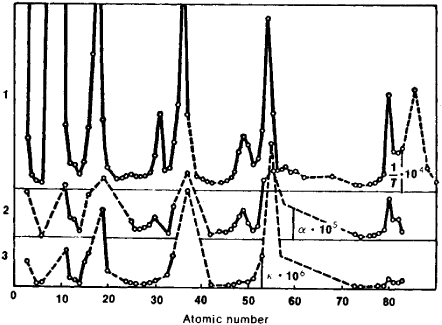
Se sabe que los electrones se organizan en capas dentro del átomo, aunque poco se sabe de la estructura geométrica de esas capas. Los gases nobles, que se encuentran en la columna del extremo derecho de la tabla periódica (Figura 1), indican que se ha completado una capa. El elmento de más a la izquierda en la fila siguiente marca en inicio de una nueva capa. Algunas propiedades como el volumen atómico, el punto de fusión, el coeficiente de expansión lineal o el facor de compresibilidad, tienen un máximo pronunciado para el número atómico correspondiente a los elementos que inician una nueva capa de electrones (3Li, 11Na, 19K, 37Rb, 55Cs). Esto se muestra gráficamente en la Figura 2.
|
(a) |
|
(b) |
|
Figura 2: (a) Dependencia del volumen atómico con respecto al número atómico (b) Variación con el número atómico de (1) la cantidad 104/T, donde T es el punto de fusión; (2) coeficiente de expansión lineal alpha·105; y (3) factor de compresibilidad K·106 (adaptada de esta referencia). |
Sin embargo, hay otros puntos destacables en esas gráficas, como son sus puntos mínimos. El Dr. Moon propone que los protones tambien se organizan en capas dentro del nucleo. Como vamos a ver en las próximas secciones, la completa ocupación de cada una de las capas de protones que él propone prácticamente se corresponden con los elementos atómicos situados en un mínimo local de las propiedades anteriores (4Be, 6C, 8O, 14Si, 26Fe, 46Pd, 92U). He añadido dos elementos al inicio de la serie, Berilio y Carbono, que no fueron originalmente propuestos por Moon, pero que también corresponden a mínimos locales y podrían encajar fácilmente en su modelo tal como explicaré más adelante.
3.- La hélice de tetraedros
Antes de entrar en detalles, voy a introducir una anlogía que nos puede ayudar a entender la lógica que existe detrás del Modelo de Moon. Consideremos cualquier juego con bolas y varillas del mismo tamaño que puedan interconectarse para formar poliedros. Empezemos con un triángulo (Figura 3a), y a cada paso añadimos un nuevo pack compuesto de una bola y tres varillas (Figura 3b). Podemos imaginar que este pack representa una partícula (nuclear) que se une a una serie de partículas nucleares ya establecidas y organizadas. El triángulo contiene tres bolas y tres varillas. Despues de añadir el primer pack, tenemos cuatro bolas y seis varillas. ¿Os resultan familiares estas cifras -es decir cuatro vértices y seis aristas del mismo tamaño? Efectivamente, ¡sólo pueden organizarse en tres dimensiones en forma de tetraedro (Figura 3c)! Además ésta es la forma más simétrica de organizar cuatro elementos en el espacio tridimensional, dejando un espacio vacío en el centro. Sugiero que los cuatro protones del nucleo de Berilio (4Be) pueden estar organizados de esa forma. Nótese que este elmento se encuentra cerca de un mínimo local de las propiedades atómicas de la Figura 2.
Vamos a añadir una nueva "partícula" (otro pack de una bola y tres varillas). Podemos ponerlo sobre cualquiera de las caras del tetraedro original, y el resultado son dos tetraedros con una cara en común (Figura 3d). Cuando añadimos un tercer pack, de nuevo podemos ubicarlo encima de cualquiera de las seis caras tetraédricas externas. El resultado es un conjunto de tres tetraedros como se muestra en la Figura 3f. Este paso completa lo que llamaremos un giro (porque sale una varilla verde de cada bola del triángulo original, empezando a definir un sentido de torsión). Un hecho interesante acerca de este conjunto de seis bolas y doce varillas del mismo tamaño es que puede reorganizarse de una forma muy simétrica ¿adivináis cual? Sí, se trata de ¡nuestro viejo amigo el octaedro (Figura 3f)!
|
(a) |
(b) |
|
(c) |
(d) |
|
(e) |
(f) |
|
Figura 3: Después de unir seis bolas usando doce varillas del mismo tamaño, el conjunto resultante de tres tetraedros puede reorganizarse en forma de octaedro. Si se considera que un tetraedro tiene un volumen unitario, el conjunto original era asimétrico y tenía un volumen de tres unidades, mientras que el octaedro resultante tiene un volumen de cuatro unidades, y además se trata una distribución perfectamente simétrica del mismo conjunto de bolas y varillas. |
|
El lector se puede estar preguntado ¿existe algún beneficio en esta reorganización? Pensando en términos de volumen, y suponiendo que cada tetredro tiene un volumen unitario, en conjunto original tenía un volumen de tres unidades, mientras que el octaedro resultante tiene un mayor volumen (cuatro unidades). Hemos alcanzado una nueva estructura que, usando la misma cantidad de "material de construcción", tiene la máxima simetría y el mayor volumen interno posible. Por lo tanto, desde este punto de vista -maximizar volumen y simetría- se trata de una estructura óptima. La estructura final también consigue el empaquetamiento óptimo de los seis elementos: una hipotética esfera circunscrita tendría un radio menor en la estructura octaédrica, con simetría central (Fig.3f), que en la estructura extendida de tres tetraedros (Figura 3e). Sugiero que la Naturaleza usa este tipo de optimización para organizar las partículas en el átomo, y en particular los protones en el nucleo atómico. Si observamos la tabla periódica de la Figura 1, esta organización octaédrica de seis protones podría corresponder al nucleo de Carbono (6C) que al igual que el Berilio se encuentra cerca de un mínimo local de las propiedades atómicas de la Figura 2.
Para continuar añadiendo packs a nuestra estructura, ahora tenemos dos opciones: o bien partir del conjunto original de tres tetraedros, o partir del octaedro reorganizado. En el primer caso, cada nuevo tetraedro puede añadirse de forma que continúe el sentido de torsión de lo que hemos llamado el primer giro. La Figura 4 muestra la hélice de tetraedros resultante despues de añadir siete packs al triángulo original, y una de sus posibles reorganizaciones simétricas. Si hubiésemos partido del octaedro reorganizado, podríamos haberlo estrellado añadiendo un tetredro a cada una de sus caras. Después de cuatro pasos, la estructura final más simétrica parece ser un tetractis (Figura 4b) o lo que Buckminster Fuller llamó un tetraedro de frecuencia doble [12]. Además de ser simétrica, esta estructura tiene un volumen de ocho unidades, en lugar de las siete unidades de volumen de la hélice de diez bolas y siete tetraedros mostrada en la Figura 4a (la misma cantidad de "material" puede reorganizarse de formas menos simétricas que alcancen volúmenes aún mayores, pero eso lo dejamos como ejercicio para el lector).
|
(a) |
(b) |
|
Figura 4: La estructura resultante de unir siete tetraedros al triángulo azul original puede reorganizarse en forma de un tetractis tridimensional. |
|
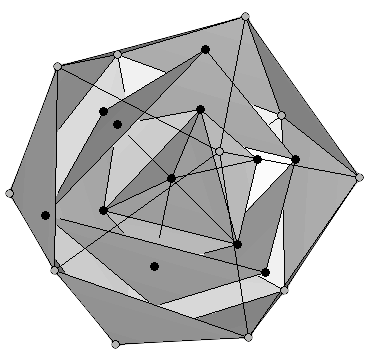
Dos tetraedros más completarían una hélice de tres giros (nueve tetraedros), que resulta contener un total de doce bolas y treinta varillas. Probablemente habréis adivinado que este material permite construir un icosaedro, que tendría un volumen máximo de 18.51 unidades en lugar de las 9 unidades de la hélice original con nueve tetraedros (Figura 5). Siguiendo este proceso, eventualmente llegaríamos a una hélice final compuesta por 33 tetraedros. El lector interesado en una interpretación alternativa de esta sorprendente estructura puede consultar la referencia [13].
|
Figura 5: Una hélice de tres giros de tetraedros contiene exactamente doce bolas y treinta varillas, así que puede organizarse de manera óptima en forma de un icosaedro perfectamente simétrico, cuyo volumen interno es máximo. |
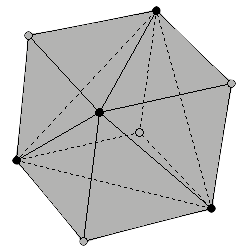
Si incrementamos el número de bolas hasta catorce, ¿dónde pondríamos las dos bolas adicionales? Una solución, que no es óptima en términos de volumen pero preserva los reordenamientos previos, se obtendría empezando por el tetractis de diez bolas de la Figura 4 y estrellando el octaedro hasta alcanzar un tetraedro estrella (Figura 6). Nótese que esta estrucutura contiene los vértices de un cubo (que se mantiene estable por los dos tetraedros "diagonales" mayores) y también los vértices de su sólido dual el octaedro. Mientras que el octaedro interno podría reflejar la distribución espacial de los seis protones en el núcleo de Carbono, el conjunto dual octaedro+cubo podría muy bien ser la distribución de los catorce protones en el nucleo de Silicio (14Si), que resulta estar cerca de otro mínimo de las propiedades atómicas de la Figura 2. La imagen que ha empezado a surgir de forma tan natural es la de protones nucleares organizados en capas: en el momento en que se ha completado una determinada capa (por ejemplo el octaedro), los protones empiezan a llenar la siguiente capa (el cubo), y así en adelante...
|
Figura 6: Una hélice de once tetraedros contiene 14 bolas y 36 varillas que pueden reorganizarse en forma de octaedro estrellado. Este es un ejemplo de una capa octaédrica rodeada por una capa hexaédrica, que podría reflejar la estructura interna de los protones en el nucleo de Silicio. |
4.- El modelo de Moon del nucleo atómico
El Dr. Robert J. Moon propuso un modelo de la distribución espacial de los protones nucleares que se puede comprender con la linea de razonamiento desarrollada en la sección previa. Antes de seguir adelante, reproduzco aquí un diálogo entre Fletcher James y el Dr. Moon acerca de la naturaleza de su modelo [1]:
"FJ: Dr. Moon, tengo una pregunta fundamental acerca de lo que hace al rellenar estos sólidos. ¿Está proponiendo una estructura en la que realmente tiene, cuantificada en el espacio, una estructura fija, con puntos, partículas que estan separadas entre ellas por intervalos fijos rígidos dentro de la estructura?
RM: No. Tenemos singularidades -singularidades en el espacio, singularidades de partículas...
FJ: ¿Pero a distancias fijas, constantes la una de la otra? ¿O está usted proponiendo que esto ocurre en un espacio de fase, y que hay una equivalencia topológica con este enrejado?
RM: Bueno, no, esto es el espacio real, por lo tanto tendría que tener un equivalente topológico. Pero esto, estas singularidades en el espacio, pueden no contener nada en su interior. Son sólo un lugar a donde las partículas pueden ir."
El Dr. Moon sugirió que la primera estructura estable en formarse era un cubo cuyos vértices definirían la distribución de los ocho protones en el nucleo de Oxígeno (8O) (Figura 7a). Después de añadir seis protones más, la siguiente capa en completarse sería un octaedro. En conjunto, pueden reflejar la distribució simétrica de los catorce protones en el nucleo de Siicio (14Si). El octaedro y el cubo forman un par dual, por lo tanto el Dr. Moon puso los vértices del cubo en los puntos medios de las caras del octaedro (Figura 7b). Estos ocho puntos están todos contenidos en la esfera inscrita del octaedro. Por tanto en realidad el cubo interno sería capaz de moverse dento de la estructura octaédrica según las fuerzas electrodinámicas actuando entre los protones. He ofrecido una distribución alternativa de estos catorce protones en la Figura 6 (volveremos a ella en la próxima sección). Como he mencionado anteriormente, el Silicio está próximo a un mínimo de las propiedades atómicas mostradas en la Figura 2.
|
(a) |
(b) |
|
Figura 7: (a) La primera capa propuesta por Moon es un cubo, el cual refleja la distribución de los ocho protones en el nucleo de Oxígeno. (b) La siguiente capa se formaría después de añadir seis nuevos protones, reflejando la distribución de los catorce protones en el nucleo de Silicio. |
|
La siguiente capa de protones propuesta por el Dr. Moon es un icosaedro. Esta se alcanza después de añadir doce nuevos protones al nucleo de Silicio (Figura 8a). Ello nos llevaría al nucleo de Hierro (26Fe) con un total de veintiseis protones. El hierro también está cerca de un mínimo de las mencionadas propiedades atómicas de los elementos. Existen muchas formas para inscribir un octaedro en un icosaedro. En la primera versión de su modelo, Moon ubicó los seis vértices del octaedro en el punto medio de seis aristas del icosaedro. Más adelante propuso ubicarlos sobre seis caras del icosaedro, de forma que dos caras octaédricas y dos icosaédricas fueran mútuamente paralelas (Figura 8b). Nótese que ninguna de estas ubicaciones del octaedro dentro del icosaedro permitiría que el primero rotara libremente. En la próxima sección propondré una alternativa que solucionaría este problema.
|
(a) |
(b) |
|
Figura 8: (a) Al completar la tercera capa en forma de un icosaedro surge la distribución de los veintiseis protones del nucleo del átomo de hierro (26Fe). (b) Los vértices del octaedro están ubicados sobre seis caras icosaédricas de tal forma que ambos sólidos tienen dos caras mútuamente paralelas. |
|
La última capa de esta estructura, como no podría ser de otra forma, sería el dodecaedro (Figura 9). Después de añadir veinte protones más al nucleo del átomo de hierro, alcanzamos la distribución de los cuarenta y seis protones del núcleo del átomo de Paladio (46Pd). Este elemento nuevamente se encuentra muy cercano al siguiente mínimo de las propiedades atómicas de la Figura 2. El icosaedro y el dodecaedro son sólidos duales, con lo cual los vértices del primero se ubicarían de forma natural sobre los puntos medios de las caras del último. Como los doce vértices del icosaedro están todos contenidos en la esfera inscrita en el dodecaedro, la estructura icosaédrica de su interior podría moverse libremente dentro de la envoltura dodecaédrica.
|
|
|
|
Figura 9: La cuarta capa en completarse forma un dodecaedro que reflejaría la distribución de los cuarenta y seis protones del nucleo de Paladio (46Pd). Los vértices del icosaedro se podrían mover libremente dentro del dodecaedro que los envuelve. |
|
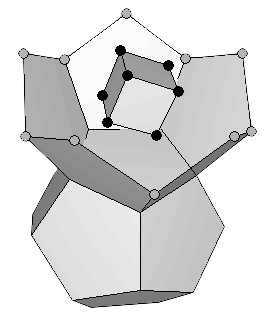
Al completar estas cuatro capas, el Dr. Moon propuso que los elementos siguientes empezaban a formar una estructura similar, gemela, encima de una de las caras dodecaédricas. Ambas estructuras compartirían los cinco vértices de esa cara, así como el vértice icosaédrico ubicado en el centro de la misma. Así que nos quedaríamos con sólo once vértices del icosaedro y quince vértices del dodecaedro. Moon hizo la hipótesis de que los primeros diez vértices que ocuparían los nuevos protones pertenecen al dodecaedro (Figura 10a). El conjunto reflejaría la distribución de protones en el nucleo del átomo de Bario (56Ba). Los ocho protones siguiente completarían el cubo interno dando lugar a la organización de los protones en el nucleo de Gadolinio (64Gd), enmedio de la série de los lantánidos (Figura 10b). Prácticamente al final de los lantánidos tenemos el átomo de Iterbio (70Yb), con una capa octaédrica completa (Figura 10c).
|
(a) |
(b) |
(c) |
|
Figura 10: (a) Moon propuso que los primeros diez protones de la estructura gemela ocupan los diez vértices del dodecaedro; la estructura refleja la distribución de protones en el núcleo de Bario (56Ba), un elemento que marca el inicio de los lantánidos. (b) Al completar el cubo interno se obtiene el nucleo de Gadolinio (64Gd). (c) Y al completar el octaedro se llega casi al final de los lantánidos en el elemento Ytterbium (70Yb). |
||
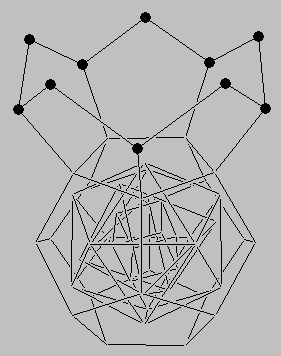
Los siguientes once protones ocuparían los vértices disponibles del icosaedro gemelo, completando otra cap y dando lugar a la disribución de los protones del nucleo del átomo de Talio (81Tl) (Figura 11a). Cinco protones más cerrarían todas las capas del dodecaedro gemelo, situándonos en el gas noble Radón (86Rd) (Figura 11b).
|
(a) |
(b) |
|
Figura 11: (a) El completar el icosaedro gemelo nos lleva al nucleo del átomo de Talio que contiene ochenta y un protones. (b) Los últimos cinco protones completan la estructura dodecaédrica gemela, la cual refleja la organización de los ochenta y seis protones dentro del nucleo del átomo del gas noble Radon. |
|
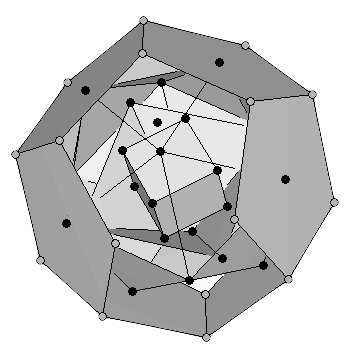
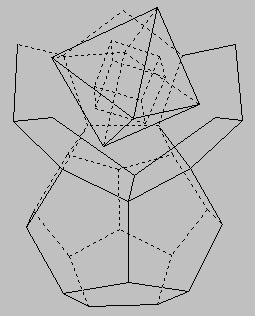
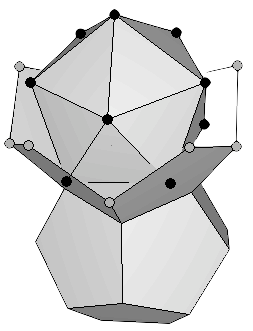
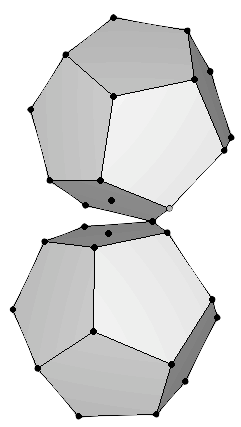
Para permitir la entrada de nuevos protones en esta estructura, el Dr. Moon observó que los dos dodecaedros se podrían separar como si estuvieran colgando de una bisagra (Figura 12a). Ello liberaría cuatro espacios que podrían ser ocupados por cuatro protones más. Dos de los cuatro elementos correspondientes, Francio (87Fr) y Actinio (89Ac) no se encuentran en la naturaleza, porque su nucleo es inestable y tiene una vida media muy corta. Han sido fabricados en reactores nucleares bombardeando elementos con neutrones. Para dejar espacio al protón nuclear del siguiente elemento, Protactinio (91Pa), el Dr. Moon propuso que la bisagra se rompe y las estructuras gemelas se mantienen unidas en un solo punto (Figura 12b).
|
(a) |
(b) |
|
Figura 12: (a) Para que los nuevos protones encuentren un lugar, el dodecaedro gemelo se debe abrir, usando una arista de la cara de unión como si fuera una bisagra. Ello hace sitio para los protones de cuatro nuevos elementos, la mayoría inestables (b) El siguiente protón se puede añadir si la bisagra se rompe y las estructuras se mantienen unidas por un sólo protón. |
|
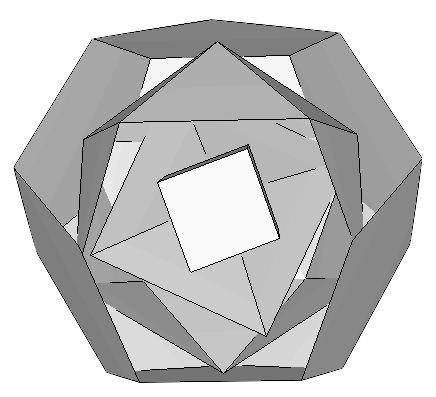
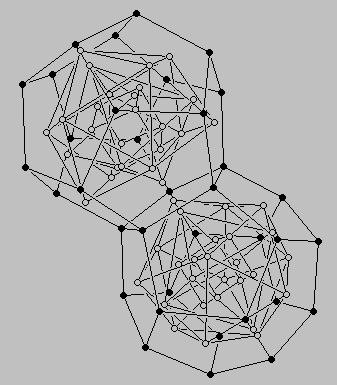
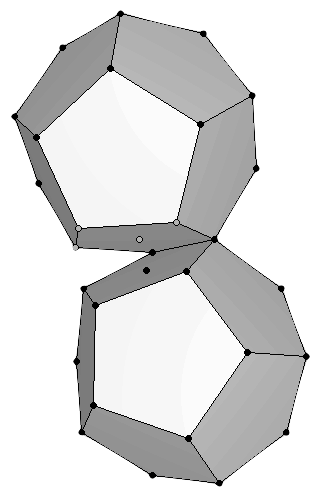
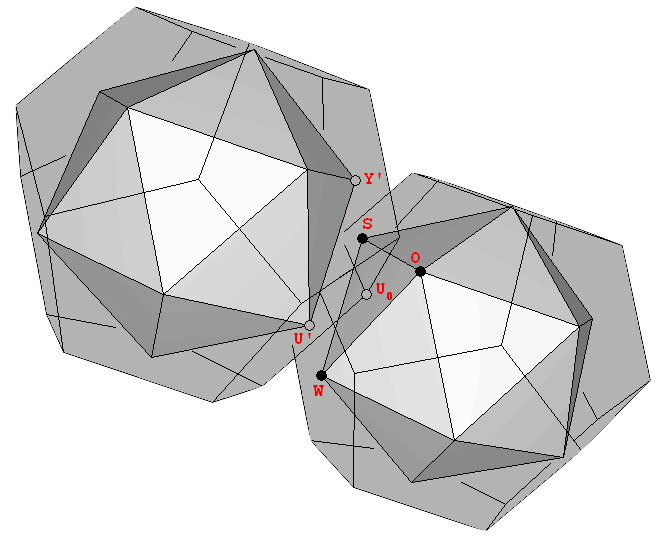
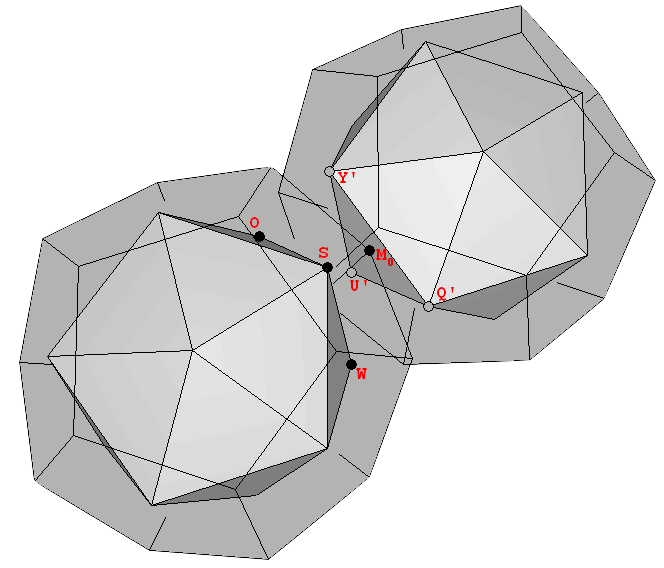
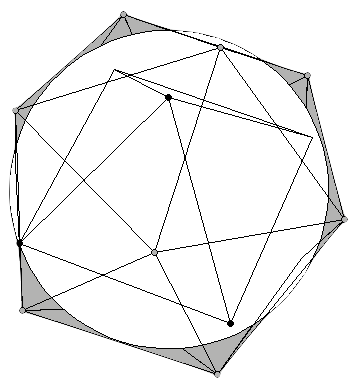
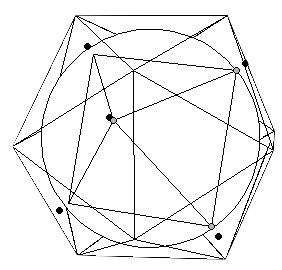
La construcción del Uranio (92U) requiere que el último protón se situe en el punto de unión. Ello se puede conseguir si la estructura se rompe, y un sólido se desplaza ligeramente para introducirse dentro del otro (Figura 13). La interpretación exacta de la estructura ilustrada en esta figura fue propuesta por Laurence Hetch, despues de definir un eje de rotación que se explicará en la próxima sección. La estructura resultante, parafraseando al Dr. Moon, "es algo que está listo para la fisión [...] si intentas poner más neutrones ahí dentro, se va a fisionar" [1]. El Dr. Robert J. Moon fue uno de los primeros científicos en conseguir la fisión nuclear en tiempos de guerra en un laboratorio ubicado debajo del campo de futbol de la Universidad de Chicago [14].
|
|
|
|
Figura 13: Dos vistas de las estructuras interpenetradas. La ubicación exacta de un vértice de cada dodecaedro en el punto medio de cada una de las caras del icosaedro opuesto explica el número y la disposición exacta de los neutrones, según explica Laurence Hetch (ver la siguiente sección). |
|
5.- Discusión
El eje del Universo
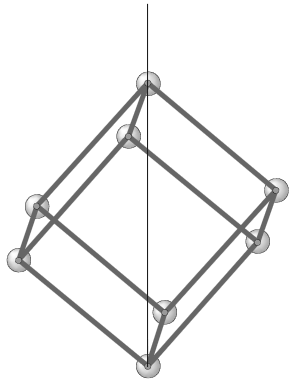
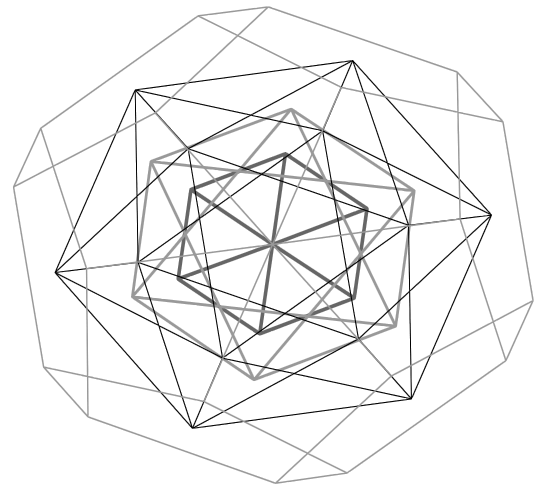
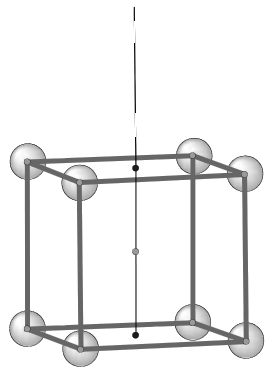
Desde la concepción original del modelo por parte del Dr. Moon, Laurence Hetch y sus colaboradores han seguido desarrollándolo más. Un aspecto interesante acerca de las propuestas de Hetch es la posible existencia de un eje preferido de rotación para el nucleo atómico. Él sugiere que este eje -al que llama el Eje del Universo- debería ser perpendicular a las caras octaédricas e icosaédricas mútuamente paralelas que se muestran en la Figura 8. De esta forma el momento angular de los protones alrededor de este eje sería mínimo en algunas de las capas, como es el caso de la capa cúbica (Figura 14). El lector interesado en las implicaciones de este eje sobre la distribución de los protones en el nucleo atómico, así com sobre las propiedades magnéticas de los elementos, puede consultar la referencia [1].
|
|
 |
 |
|
|
Figura 14: Vista superior del modelo de Moon desde el Eje del Universo propuesto por L. Hetch. Nótese que el eje es diagonal al cubo y al dodecaedro, pero no al icosaedro ni al octaedro. |
|||
Rotación libre de cada capa
Los vértices del icosaedro, aunque originalmente se ubicaronen el centro de las caras dodecaédricas, no necesitan estar ahí en absoluto. De hecho la estructura icosaédrica completa podría rotar libremente dentro de la estructura dodecaédrica, con el objeto de alinearse de la mejor forma con respecto al eje de rotación preferido. Sin embargo, eso mismo no podría suceder con la estructura octaédrica, puesto que en el modelo original de Moon sus vértices sobrepasan la esfera inscrita en el icosaedro (Figura 15a). Sugiero que esta limitación se puede superar reduciendo la distancia de los vértices del octaedro al centro de la estructura -y la de los vértices del cubo proporcionalmente- de manera que la esfera circunscrita del octaedro coincida con la esfera inscrita del icosaedro (Figura 15b). Con este simple ajuste, las cuatro capas podrían rotar la una dentro de la otra, obviamente restringidas por las fuerzas electrodinámicas entre sus protones.
|
(a) |
(b) |
|
|
Figura 15: (a) La esfera circunscrita del octaedro en el modelo original de Moon es más grande que la esfera inscrita en el icosaedro. (b) Acercando ligeramente los vértices del octaedro al origen ambas esferas coincidirían, permitiendo así que el octaedro girase libremente dentro del icosaedro. |
||
¿Se llena primero la capa octaédrica?
El orden en el que se llenan las dos primeras capas -hexaédrica y octaédrica- merece un poco más de discusión. El lector atento se habrá dado cuenta de que el elemento Oxígeno (8O), cuyos protones nucleares están organizados en forma de un cubo según el modelo de Moon, no representa un mínimo de las propiedades atómicas de la Figura 2. Yo sugiero que ello se puede explicar fácilmente alterando el orden en que se llenan las dos primeras capas. Tal como he comentado en la sección 3, los primeros cuatro protones del nucleo probablemente están organizados en forma de tetraedro. Ello correspondería al nucleo del átomo de Beryllium (4Be), que se encuentra cerca del primer mínimo de las propiedades atómicas antes mencionadas. El siguiente protón, (el quinto) no tendría un sitio fijo que ocupar, pero cuando se alcanza la cifra de seis protones, es probable que el conjunto se reorganize en forma de un octaedro, y ello correspondería al núcleo del átomo de Carbono (6C). Este elemento también está cerca de un mínimo de las propiedades atómicas de la Figura 2, mucho más cerca de lo que está el Oxígeno. El próximo mínimo pronunciado aparece en el Silicio (14Si), que como ya se ha mencionado completaría el cubo y su dual el octaedro. Cual de los dos está dentro del otro no está claro. El Dr. Moon propuso que el cubo iba dentro del octaedro, pero como acabo de argumentar también podría ser al revés.
¿Y qué sucede con los neutrones?
El nucleo atómico no solo consiste de protones cargados positivamente; también contiene partículas neutrales, los neutrones. El modelo de Moon no explica la ubicación de los neutrones dentro del nucleo. De hecho, el propio Dr. Moon solía decir: "los protones encuentran su plaza de aprcamiento en lo que correspondería a los vértices. Y luego los neutrones, que también están ahí fuera, no nos tenemos que preocupar de ellos, porque no tienen carga y pueden encontrarse prácticamente ne cualquier parte" [6]. Sin embargo, Larry Hetch también ha trabajado este aspecto y esencialmente propone que los neutrones pueden ocupar los puntos medios de las aristas de los sólidos platónicos encajados, así como el centro de las caras icosaédricas no ocupadas ya por protones [13]. El nucleo de Uranio-238 proporciona una evidencia directa a favor de su propuesta. Hemos visto que en el nucleo de uranio las dos estructuras dodecaédricas se interpenetraban una a la otra. El número de aristas y centros de caras libres para ser ocupadas por neutrones son:
| Caras del cubo | 6 |
| Aristas del cubo | 12 |
| Aristas del octahedro | 12 |
| Aristas del icosaedro | 30 |
| Caras del icosaedro | 13 |
| TOTAL | 73 |
Esto dejaría posiciones para 73 neutrones en cada estructura gemela ¡¡precisamente el número correcto para los 146 neutrones del Uranio-238!! Además, nótese que el cambio de orden en el que se llenan las primeras capas que yo he propuesto no alteraría esta cuenta, ya que las dos caras adicionales del icosaedro ocupadas por los dos vértices extra del cubo se compensarían con las dos caras extra del octaedro en la capa más interna, con lo cual el total sería el mismo:
| Caras del octaedro | 8 |
| Vértices del octaedro | 12 |
| Aristas del Cubo | 12 |
| Aristas del Icosaedro | 30 |
| Caras del Icosaedro | 11 |
| TOTAL | 73 |
Actualizado el 21/03/2013
REFERENCIAS
[1] Hetch L., Stevens Ch.B.: "New Explorations with The Moon Model".
[2] Hetch L.: "Who was Robert J. Moon?".
[3] Tsimmerman V.: "Perfect Periodic Table".
[4] Assis A.K.T., TorresSilva, H.: "Comparison between Weber's electrodynamics and classical electrodynamics".
[5] Hetch L.: "The Atomic Science textbooks don't teach".
[6] Hetch L.: "The Life and Work of Dr. Robert J. Moon".
[7] Bacciagaluppi G., Valentini A..: "Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference".
[8] Bohm D., Hiley B.J., Kaloyerou P.N.: "An Ontological basis for the Quantum Theory".
[9] Correa P.N., Correa A.N.: "The Electric Aether and the Structure of the Electron".
[10] Ginzburg V.B., "Three-Dimensional Spiral String Theory".
[11] De-Picciotto R. et al., "Direct observation of a fractional charge".
[12] Edmondson A.C., "A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller".
[13] Kappraff J., "The Flame-Hand letters of the Hebrew Alphabet".
[14] Hetch L.: "The Geometric Basis for the Periodicity of the Elements".