- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
La Proporción Aurea
1.- Introducción
De forma simple, la Proporción Aurea establece que lo pequeño es a lo grande como lo grande es al todo. Habitualmente esto se aplica a las proporciones entre segmentos. Esta razón ha sido venerada por toda cultura en este planeta. Podemos encontrarla en el arte, la composición musical, incluso en las proporciones de nuestro propio cuerpo, y en general en toda la Naturaleza "escondida" detrás de la secuencia de Fibonacci. En este sitio también proporcionamos algunos ejemplos de disciplinas en donde la presencia de la Proporción Aurea resultaba insospechada hasta hace poco. Este es el caso, por ejemplo, de la Física Atómica o la población de los codones del ADN del genoma humano completo.
Es este artículo voy a presentar lo básico sobre la Proporción Aurea. Como no me gusta dar las cosas por supuestas, tampoco espero que tu lo hagas. Por lo tanto, intentaré proporcionar demostraciones matemáticas o geométricas cortas de mis afirmaciones (no temas, no te vas a enfrentar a ninguna ecuación diferencial en derivadas parciales). Vamos a hablar sobre la definición de la Proporción Aurea, su construcción geométrica, algunas propiedades matemáticas, y algunos objetos geométricos importantes donde se puede encontrar. Las "aplicaciones" se dejan para las páginas separadas que puedes encontrar en la sección "Y mucho más...", aunque te recomiendo leer este artículo primero.
2.- La Proporción Aurea como un valor límite
Es importante enfatizar que, aunque los Griegos dieron a la Proporción Aurea su nombre Phi (φ), como su nombre indica en realidad es una razón o cociente. Esta razón puede obtenerse en forma de límite del tipo de sucesión general siguiente (nos dimos cuenta de esta propiedad al ller la web de R.W. Ray). Dados dos elementos iniciales positivos a0 y a1, calculamos el elemento general an como la suma de los dos elements precedentes:
Como consecuencia, la razón de dos elementos consecutivos de la sucesión también sigue una sucesión:
Si las razones consecutivas qn tienden a un valor límite Q, este tiene que satisfacer la ecuación
Ello nos lleva a la conocida ecuación de segundo grado cuya solución positiva es φ:
Lo que este resultado nos indica es que la razón entre dos valores consecutivos de cualquier sucesión de este tipo siempre se aproxima a φ. Notad que la Proporción Aurea está conectada con la forma como se construye la sucesión, pero no con ningún ejemplo particular de esa construcción. Podríamos proponer un número infinito de sucesiones de ese tipo dependiendo de los valores iniciales a0 and a1. Por ejemplo, cuando a0=2 y a1=1 obtenemos la Sucesión de Lucas:
| n | L(n) | qn = L(n)/L(n-1) |
| 1 | 2 | --- |
| 2 | 1 | 1/2 = 0.500 |
| 3 | 3 | 3/1 = 3.000 |
| 4 | 4 | 4/3 = 1.333 |
| 5 | 7 | 7/4 = 1.750 |
| 6 | 11 | 11/7 = 1.571 |
| 7 | 18 | 18/11 = 1.636 |
| 8 | 29 | 29/18 = 1.611 |
| 9 | 47 | 47/29 = 1.620 |
| 10 | 76 | 76/47 = 1.617 |
|
Tabla 1: El cociente de elementos consecutivos de la sucesión de Lucas converge a la Proporción Aurea. |
||
Pero hay una sucesión muy especial que está íntimamente relacionada con la Proporción Aurea, y esta es la Sucesión de Fibonacci (a0=1, a1=1):
| n | F(n) | qn = F(n)/F(n-1) |
| 1 | 1 | --- |
| 2 | 1 | 1/1 = 1.000 |
| 3 | 2 | 1/2 = 0.0500 |
| 4 | 3 | 3/2 = 1.500 |
| 5 | 5 | 5/3 = 1.666 |
| 6 | 8 | 8/5 = 1.600 |
| 7 | 13 | 13/8 = 1.625 |
| 8 | 21 | 21/13 = 1.615 |
| 9 | 34 | 34/21 = 1.619 |
| 10 | 55 | 55/34 = 1.617 |
|
Tabla 2: El cociente de elementos consecutivos de la sucesión de Fibonacci converge a la Proporción Aurea. |
||
¿Y por qué es tan especial la sucesión de Fibonacci? Bien, al menos por el hecho de que, como Drunvalo Melchizedek apunta en su primer libro "El antiguo secreto de la Flor de la Vida", la Naturaleza utiliza esta propiedad para construir sucesiones de longitudes que convergen a la Proporción Aurea, como son las distancias entre ramas sucesivas de un árbol, o las hojas sucesivas en una rama, o las dimensiones de nuestro propio cuerpo:
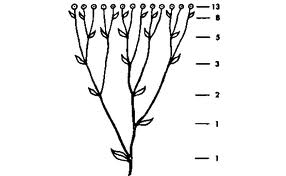 |
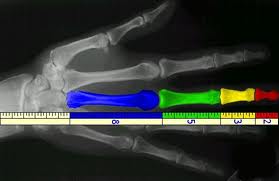 |
| Figura 1: Dos ejemplos de construcciones naturales que obedecen a la sucesión de Fibonacci. | |
La sucesión de Fibonacci tiene muchas más propiedades interesantes y está más involucrada en nuestra percepción de la realidad de lo que sospechamos. Estamos preparando un artículo sobre este punto que estará disponible pronto en la sección correspondiente de este sitio.
Antes de seguir adelante, deberíamos apuntar algunas propiedades matemáticas que se desprenden del hecho que φ satisface la ecuación de segundo grado φ2 = φ + 1:
| Indice | Potencia | Inverso |
| 1 | φ | 1/φ = φ - 1 |
| 2 | φ2 = φ + 1 | 1/φ2 = 1 - 1/φ = 2 - φ |
| 3 | φ3 = φ2 + φ = 2φ + 1 | 1/φ3 = 1/φ-1/φ2 = 2φ - 3 |
| 4 | φ4 = φ3 + φ2 = 3φ + 2 | 1/φ4 = 1/φ2-1/φ3 = 5 - 3φ |
| 5 | φ5 = φ4 + φ3 = 5φ + 3 | 1/φ5 = 1/φ3-1/φ4 = 5φ-8 |
| ... | ... | ... |
| n | φn = φn-1 + φn-2 = F(n)φ + F(n-1) | 1/φn = 1/φn-2-1/φn-1 = (-1)n·[F(n+1) - F(n)φ] |
|
Tabla 3: Potencias de la Proporción Aurea |
||
donde F(n) es el n-ésimo elemento de la sucesión de Fibonacci que empieza como F(0) = F(1) = 1.
A propósito, es inmediatamente aparente a partir de la Tabla 3 que la propia φ sigue una sucesión de "Fibonacci", la cual al mismo tiempo es una progresión geométrica, tanto por encima como por debajo de la unidad:
3.- La Proporción Aurea como un valor medio
La Proporción Aurea es también una forma de dividir un segmento en dos partes que reproducen la afirmación hecha al inicio de este artículo: lo pequeño es a lo grande como lo grande es al todo. Considerad el segmento siguiente:
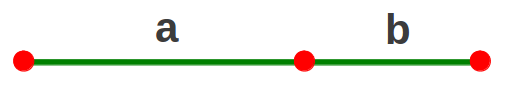
Su división según la Proporción Aurea puede expresarse matemáticamente como sigue:
Esta relación puede tratarse en términos del cociente Q=a/b, lo cual nos conduce a la misma ecuación que antes:
De ello deducimos que cada parte (la parte grande a o la parte pequeña b) representan las proporciones siguientes con respecto al segmento total (a+b):
En el caso especial de un segmento unitario, la Proporción Aurea proporciona la única forma de dividir la unidad en dos partes que están en progresión geométrica:
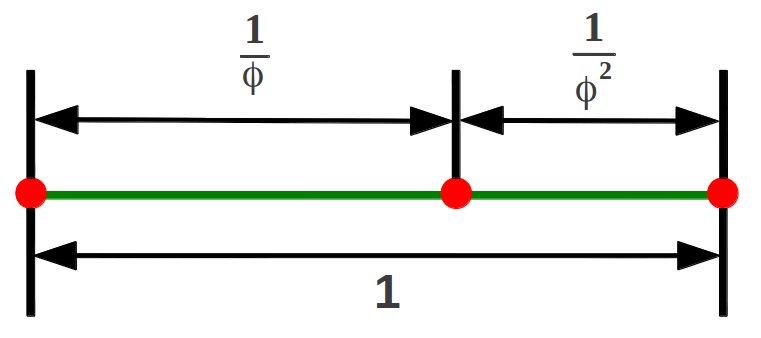 |
| Figura 2: La Proporción Aurea es la única forma de dividir la unidad en dos partes que están en progresión geométrica. |
Antes de entrar en los métodos de construcción geométrica, me gustaría enfatizar otro hecho: la división de un segmento según la Proporción Aurea es un proceso que puede iterarse de forma indefinida, y la primera división proporciona todos los elementos necesarios para hacerlo. La figura siguiente ilustra el proceso de división iterada en Razones Aureas sucesivas. Este proceso también puede iterarse hacia el exterior usando las potencias crecientes de φ (ver Tabla 3):
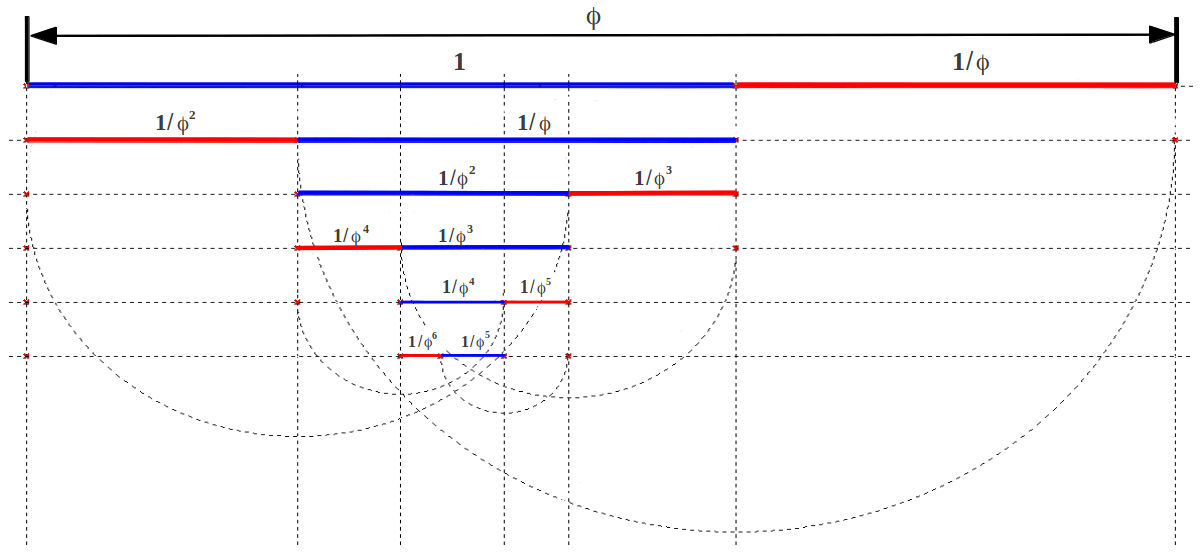 |
| Figura 3: División iterada de un segmento según la Proporción Aurea. |
4.- Métodos de construcción geométrica
Hay muchas formas de dividir un segmento geométricamente siguiendo la Proporción Aurea. Todos ellos solo necesitan una regla y un compás (¡ninguno calculadora científica!). Vamos a mostrar tres de ellos. En el primero (Método A, Figura 4) tan solo necesitas calcular el punto medio de un segmento dos veces: empezando por el segmento AA', se calcula su punto medio M. Entonces se marca el punto B de forma que el segmento MB tenga la misma longitud que AA', y se calcula su punto medio M'. Por último, se marca el punto C tal que M'C=MB y esto es todo. Uno acaba con un segmento AC que está dividio según los Segmentos Aureos AB y BC. Es decir,
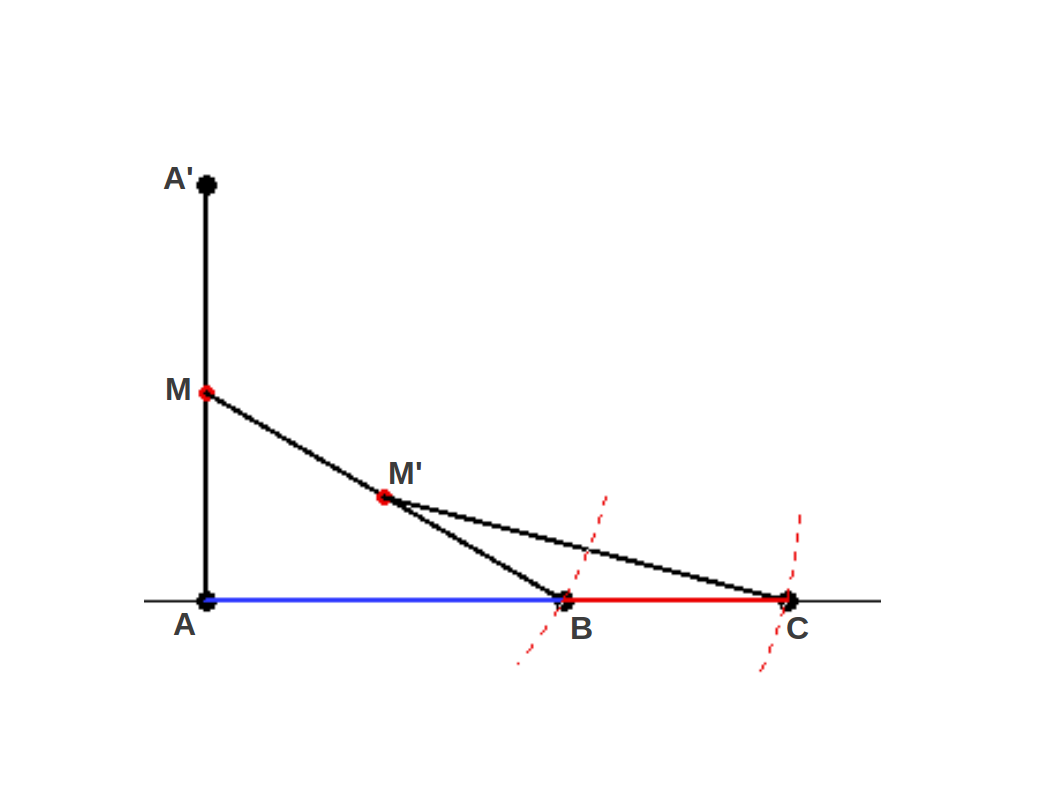 |
| Figura 4: METODO A: Construcción geométrica de la Proporción Aurea usando dos puntos medios. Con este método, no se sabe a priori la longitud del segmento AC. |
Los otros dos métodos tienen en común el uso de un triángulo 1-1/2 (es decir, un triángulo rectángulo con un cateto de longitud doble del otro). En el método B se empieza por el segmento AC y se calcula su punto medio M (Figura 5). Entonces se levanta la mitad de ese segmento perpendicularmente a MC para obtener el punto C' y el triángulo 1-1/2 ACC' (cuya diagonal es ). Entonces se lleva la altura del triángulo sobre la hipotenusa AC' para obtener el punto B', y por último se lleva la longitud AB' hacia abajo para obtener el punto B, que divide el segmento original AC según la Proporción Aurea, con lo cual tenemos de nuevo:
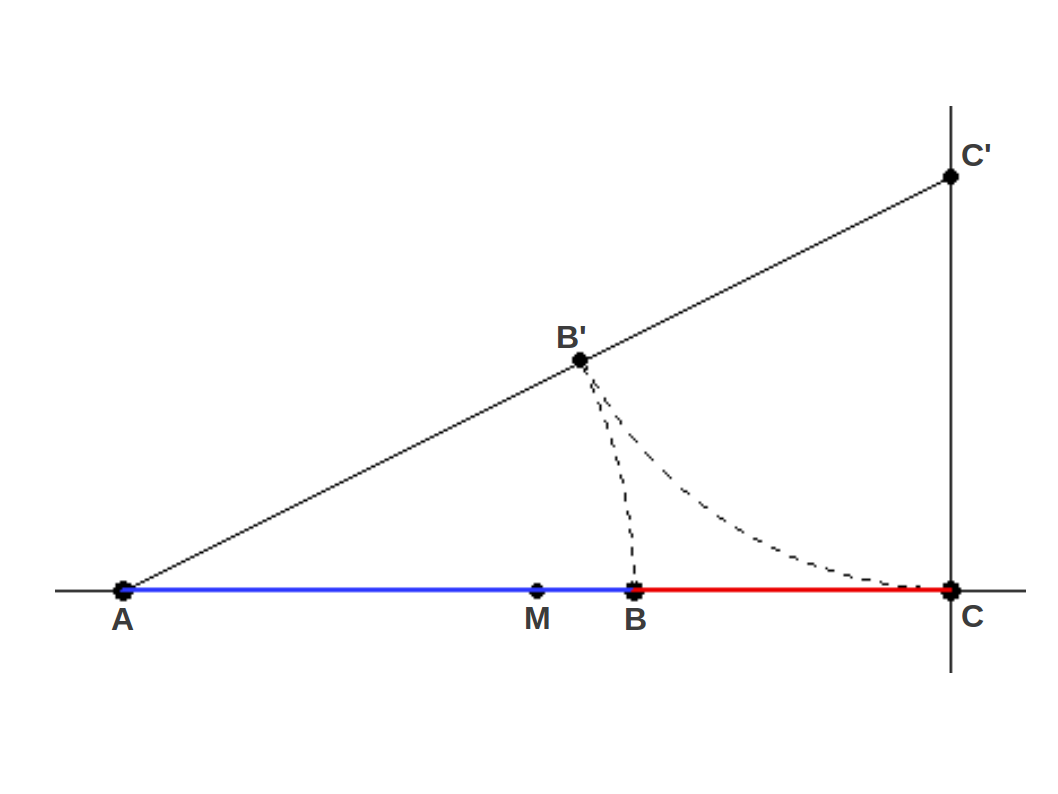 |
| Figura 5: METODO B: División geométrica de un segmento según la Proporción Aurea usando dos arcos. El segmento original acaba dividido en dos partes Aureas. |
El tercer método (método C) empieza por un cuadrado de lado AB (Figura 6). Se calcula el punto medio de este lado y se dibuja un círculo con centro en este punto pasando por D hasta encontrar el punto C. Y ya lo tenemos: el segmento AC está dividido según la Proporción Aurea en el punto B, así que tenemos de nuevo
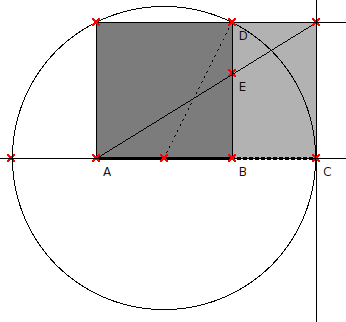 |
| Figure 6: METODO C: Determinación geométrica de un segmento AC tal que AB y BC están en Proporción Aurea. El proceso produce un Rectángulo Aureo, que contiene un cuadrado y un Rectángulo Aureo más pequeño dentro. |
El tercer método tiene la ventaja de que se acaba con un Rectángulo Aureo, eso es, un rectángulo cuyos lados están relacionados por la Proporción Aurea. Y este proceso se puede iterar indefinidamente sin necesidad de ningún nuevo círculo, simplemente dibujando las diagonales de cada rectángulo. Por ejemplo el rectángulo Aureo pequeño de la Fig.6 (gris claro) contiene un rectángulo Aureo aún menor determinado por el punto E, que divideel lado BD en dos partes Aureas BE y ED (el lector debe notar que en un rectángulo general las longitudes BE y BC no son necesariamente iguales, mientras que en un rectángulo Aureo sí lo son). Así pues, cada nuevo rectángulo Aureo en este proceso iterativo se compone de un cuadrado y un nuevo rectángulo Aureo menor. Este proceso constructivo permite construir la Espiral Aurea:
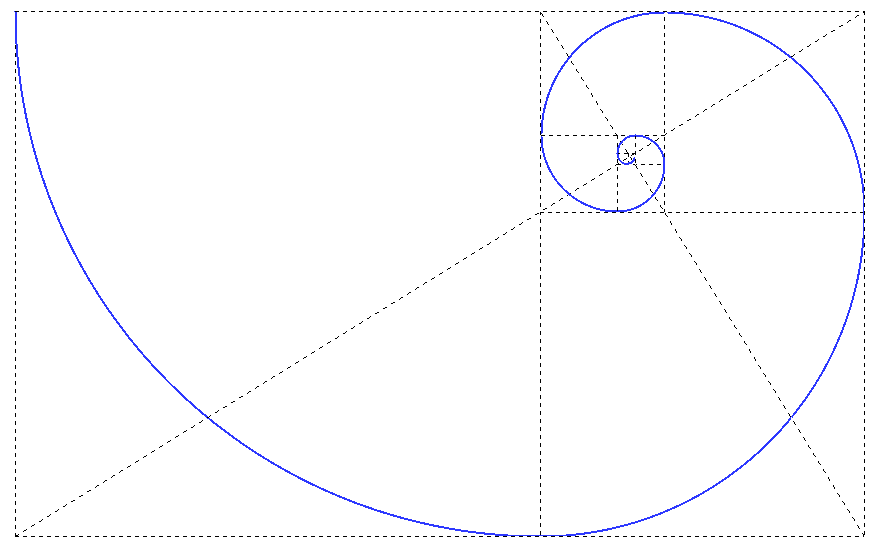 |
| Figura 7: La Espiral Aurea |
A pesar de que los tres métodos geométricos de construir φ son equivalentes, cada uno tiene su uso preferido. Por ejemplo, el método B se usa cuando uno quiere dividir un segmento de longitud conocida en subsegmentos que obedecen la Proporción Aurea. Por el contrario, el método C empieza por un segmento que acabará siendo la parte grande de la división de el segmento total AC en Razón Áurea. El Método A puede usarse cuando no se tiene ningún segmento que dividir pero simplemente se necesita la proporción. Entonces éste se puede trasladar a cualquier segmento deseado por similitud.
5.- Triángulo Aureo y Gnomon Aureo
La Proporción Aurea aparece en muchas cosntrucciones geométricas. Una de ellas es el Triángulo Aureo. Es un triángulo isósceles cuyos lados laterales están en proporción Aurea con la base, que habitualmente se toma como la unidad (Figura 8). ¿Cual es el valor del ángulo θ? Podemos calcularlo, pero lo vamosa deducir en la siguiente figura.
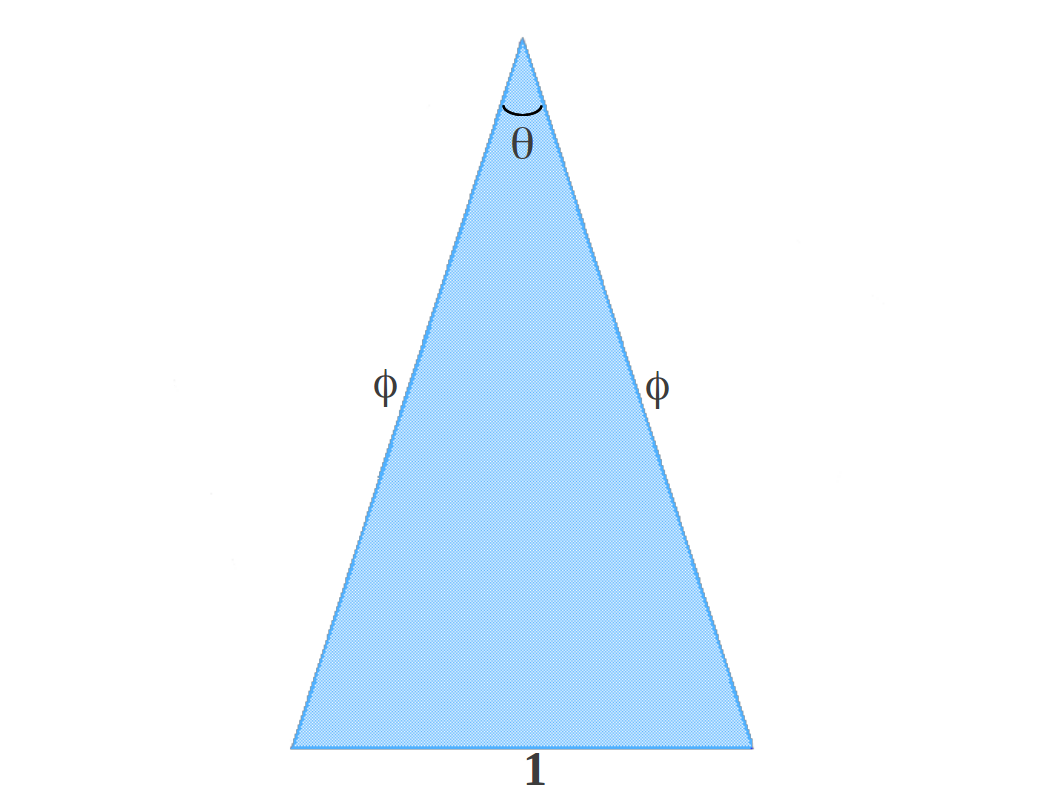 |
| Figura 8: El Triángulo Áureo |
Cuando extendemos un arco desde la base de este triángulo hacia arriba, aparece otro triángulo isósceles dentro del anterior. Esta construcción se suele llamar el Gnomo Aureo. Aquí lo mostramos antes de determinar los valores de los distintos ángulos y de la longitud del lado L (Figura 9).
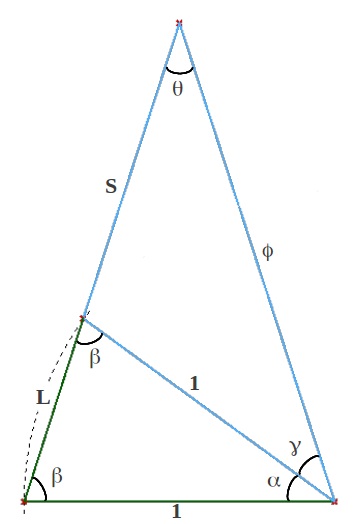 |
| Figura 9: El Gnomon Aureo (preliminar) |
Del hecho que el triángulo grande exterior y el triángulo pequeño interior son ambos isósceles y comparten dos ángulos iguales β, se deduce que α = β. Es decir, los triángulos interior y exterior son similares porque tienen los mismos ángulos. Esto significa que la base del triángulo interno obedece la similitud:
Por lo tanto
con lo cual en triángulo superior azul también es isósceles. Ello implica que γ = θ, de forma que en realidad el segmento azul interno de longitud 1 bisecta el ángulo β de la derecha. Esta propiedad también permite determinar el valor de los ángulos β y θ en el Triángulo Aureo:
Ello nos lleva a la figura del Gnomon Aureo que se puede encontrar en todas partes:
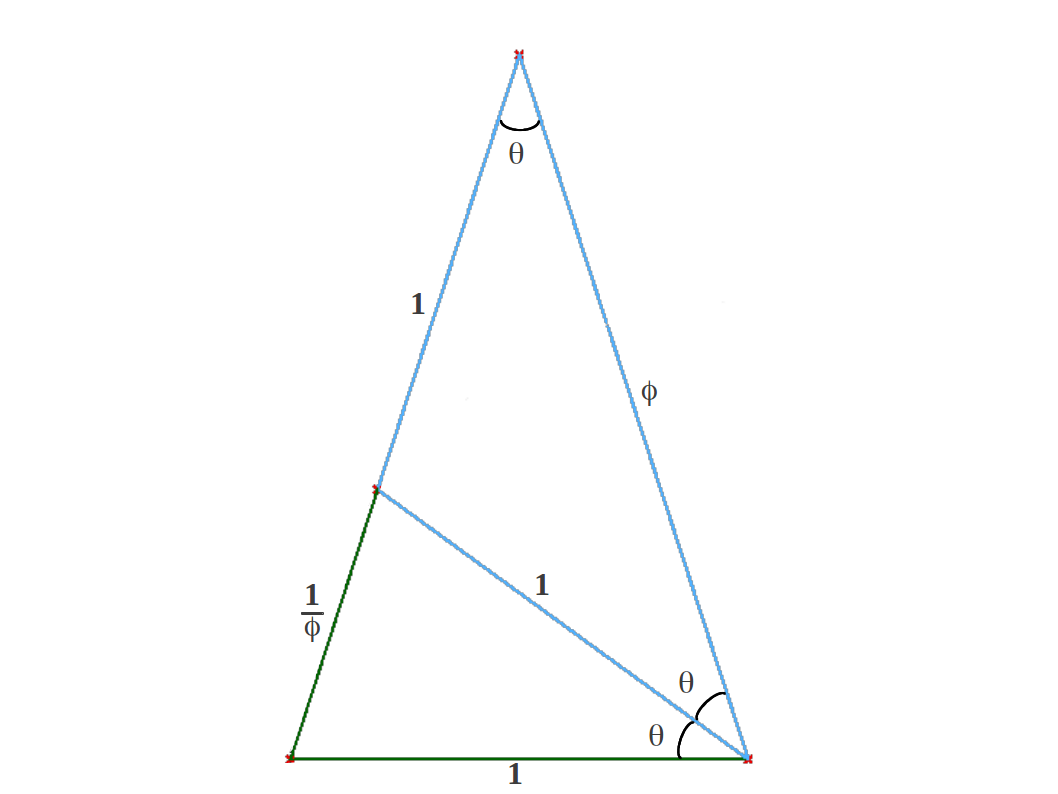 |
| Figura 10: El Gnomon Aureo |
6.- La Proporción Aurea en el pentágono
El pentágono es el polígono regular que contiene de forma natural la Proporción Aurea. Parafraseando a Lawlor [1] "el pentágono [es] el símbolo de la vida, con su simetría quíntuple que sólo aparece en los organismos vivos". En realidad el pentágono podría definirse como el polígono regular de cinco lados cuyas diagonales están en Proporción Aurea con sus lados. Esta propiedad proporciona un método directo de construir un pentágono como se muestra en la figura siguiente:
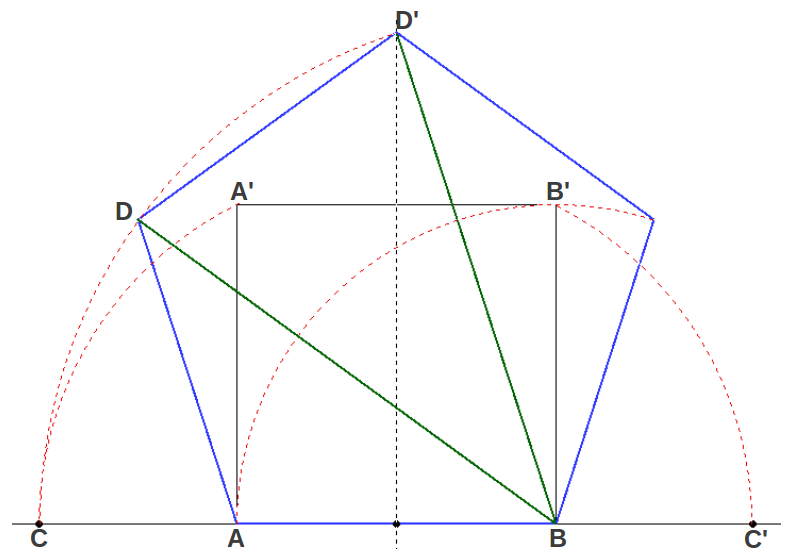 |
| Figura 11: La construcción del pentágono a partir de la Proporción Aurea. |
Empezando por el lado AB, se calculan los puntos C y C' que extienden este segmento en Proporción Aurea (CB/AB = AC'/AB = φ). Entonces la longitud BC se convierte en la diagonal del pentágono (por ejemplo BD y BD' en la figura) y permite localizar sus vértices (Figura 11).
El Triángulo Aureo y el Gnomon Aureo están contenidos de forma natural dentro del pentágono (Figura 12). Esto demuestra de una forma diferente que en el pentágono la razón entre la diagonal y el lado es φ.
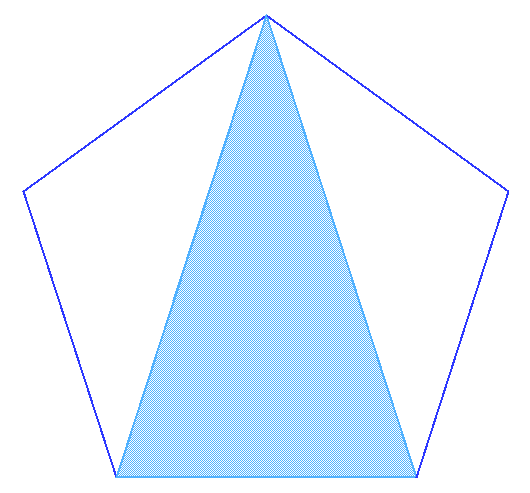 |
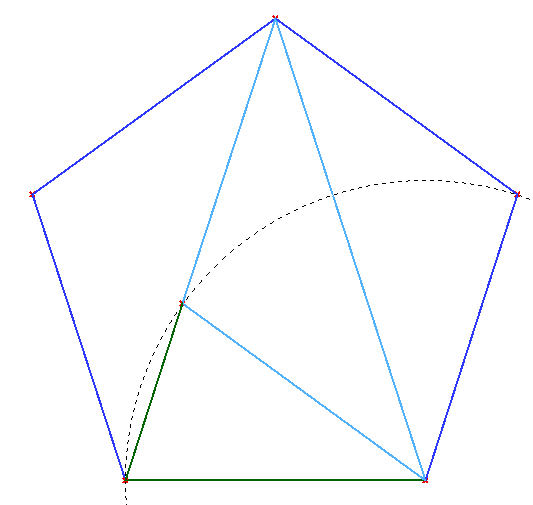 |
| (a) Triángulo Aureo en el pentágono | (b) Gnomon Aureo en el pentágono |
| Figura 12 | |
Cuando se dibujan todas la diagonales del pentágono se consigue un pentagrama. El pentagrama muestra que el Gnomon Aureo, y por lo tanto la Proporción Aurea, están contenidos iterativamente dentro del pentágono (Figura 13).
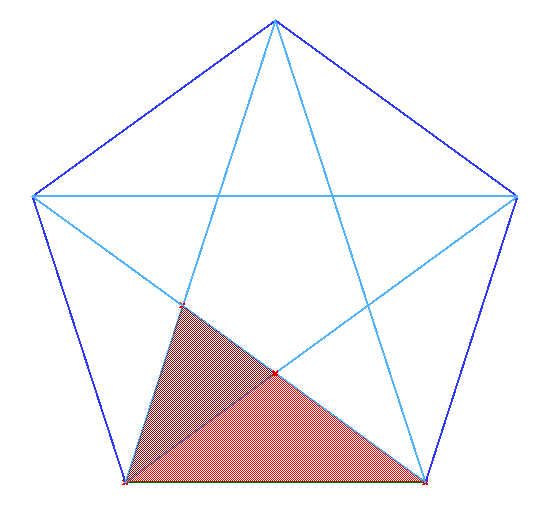 |
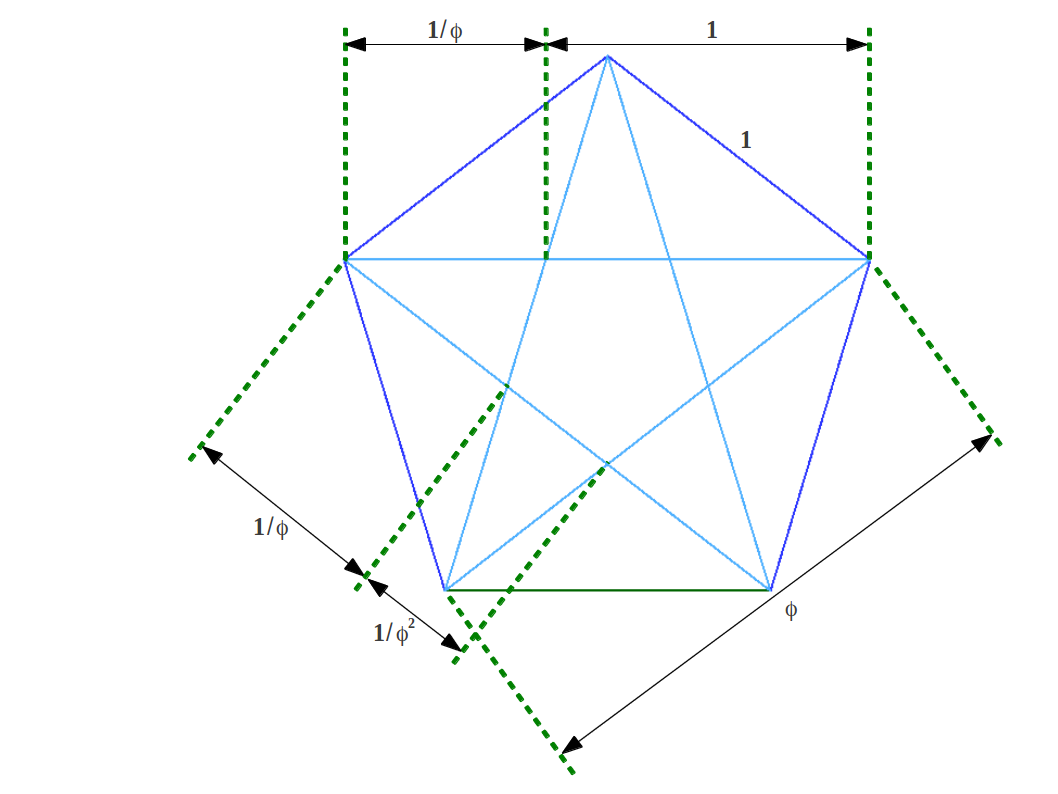 |
| (a) Gnomons Aureos iterados en el pentágono. | (b) Proporciones sucesivas en Proporción Aurea en el pentagrama. |
| Figure 13 | |
Me gustaría finalizar esta introducción a la Proporción Aurea mostrando una construcción geométrica que esconde muchas proporciones de la Geometría Sagrada. Se trata de la cuadratura del círculo analizada en [1] (Figura 14).
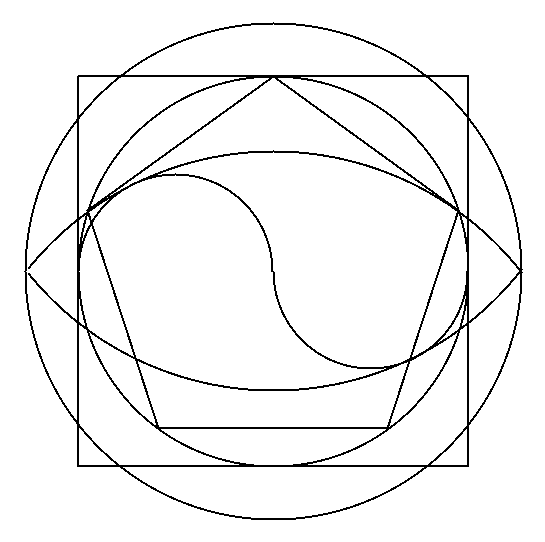 |
| Figura 14: La cuadratura del círculo. |
Dejamos como ejercicio para el lector el cálculo de las proporciones Aureas contenidas en esta construcción (Figura 15). Cabe destacar que el cuadrado y el círculo exteriores tienen prácticmente el mismo perímetro, y éste está relacionado con una relación sencilla largamente conocida entre dos números generatrices maestros como son φ y π.
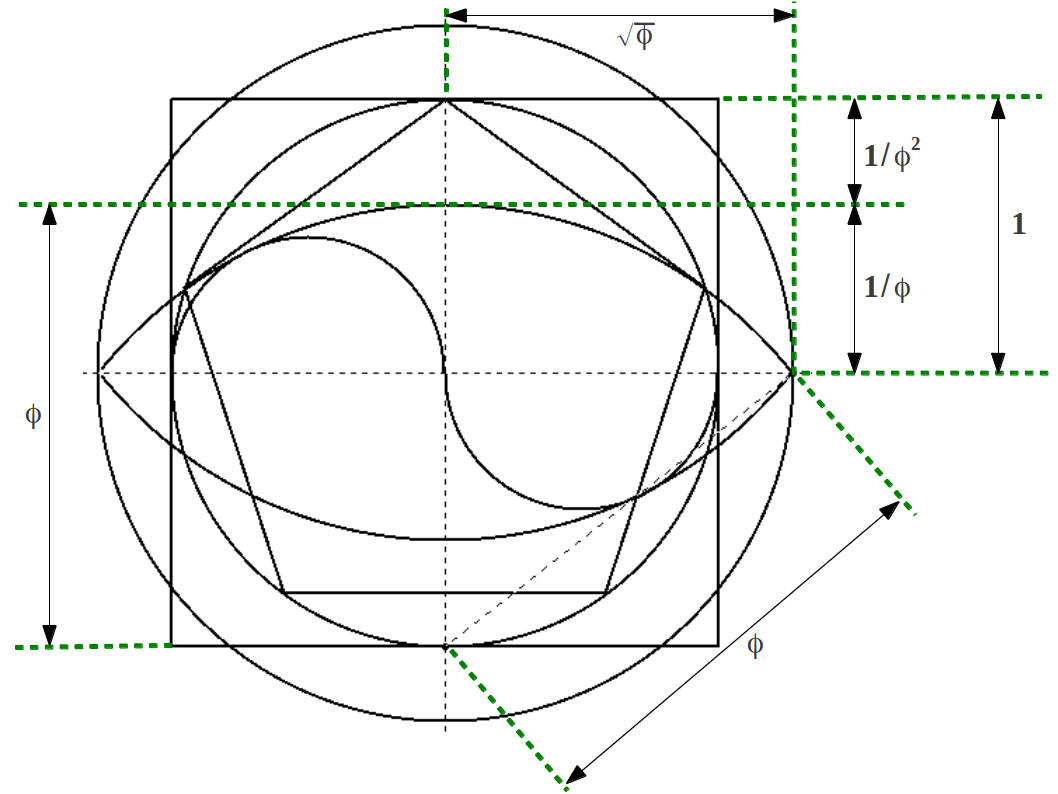 |
| Figura 15: Proporciones Aureas en la cuadratura del círculo. |
7. Referencias
Lawlor, Robert: "Sacred Geometry. Philosophy and Practice", Thames and Hudson, 1982, ISBN 0-500-81030-3.
