- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Sobre la frecuencia de afinación A=432 y c=128
Ultima actualización:
01/09/2013
Tabla de Contenido
1.- Introducción
2.- Comparando las escalas a las frecuencias de afinación A=440 and A=432
3.- Experimentos con las frecuencias de tonos individuales
4.- Frecuencias de afinación para los Modos Aulós griegos
5.- Sobre las cualidades ocultas de un tono
6.- Referencias
1.- Introducción
En la primera parte de este artículo describíamos en detalle la estructura de las escalas musicales antiguas y modernas. Se compararon las escalas y se describieron algunas diferencias auditivas cualitativas en el sonido de intervalos similares pertenecientes a escalas distintas. Las escalas definen los intervalos entre las frecuencias de todas las notas de una octava. La frecuencia de cada nota habitualmente se da de forma normalizada: está referenciada a la frecuencia de la primera nota, la llamada tónica. Una vez que se ha fijado la frecuencia de una nota, la frecuencia del resto de las notas de la escala también queda fija, según los intervalos relativos dados por la estructura de la escala en cuestión.
Los instrumentos modernos se afinan fijando no la tónica, sino la sexta nota de la escala a una frecuencia A=440Hz. En la última sección, explicamos los hallazgos prácticos de la violinista e investigadora Maria Renold cuando tocaba música en su nueva escala de doce quintas. Ella observó de forma reiterada que si se utiliza la frecuencia de afinación A=440Hz los intervalos y los tonos se convierten en antisociales, y además causan que las personas se provoquen las unas a las otras. Por el contrario, los intervalos y los tonos tienen un efecto placentero y armónico cuando se afinan a la frecuencia A=432Hz. Las comparaciones se hicieron durante muchos años y en muchos sitios, y siempre se producía el mismo fenómeno. Estos hallazgos demuestran que los tonos de determinadas frecuencias poseen cualidades características que pueden tener efectos mayores sobre el ser humano.
Para descartar la posibilidad de que este comportamiento sólo se produjera en su escala en particular, llevó a cabo una serie de experimentos auditivos en más de 2000 personas de distintos paises, comparando parejas de tonos individuales obtenidos con ambos métodos de afinación (A=440Hz y A=432Hz). De esta forma eliminó la influencia de la estructura de intervalos de cualquer escala. Los resultados fueron sorprendentes: práticamente toda la gente apreció cualidades distintas individuales e inconfundibles entre tonos que representaban la misma nota musical en los dos métodos de afinación. Alrededor del 90% de la gente encontró que los tonos procedentes del método de afinación A=440Hz sonaban incómodos, desagradables e irritantes, mientras que los tonos procedentes de la afinación A=432Hz sonaban tranquilos, agradables y llenos. Se hicieron muchas comparaciones utilizando instrumentos distintos con los mismos resultados, lo que parece indicar que la cualidad individual de cada tono se origina en el propio tono, y no en los intrumentos con los que se toca. De forma independiente a esta autora, diversos músicos y maestros han realizado observaciones similares. Otro punto clave es que conviene tocar los tonos en un instrumento no eléctrico: Maria Renold observó que de lo contrario se pierden las cualidades inherentes de cada tono. En el resto del artículo se proporcionan más detalles al respecto. Se presentan también las frecuencias de afinación recomendadas para los Modos Aulós griegos. Finalmente discutimos acerca del posible origen de las cualidades ocultas de un tono que los seres humanos somos capaces de percibir, pero aun no de medir.
2.- Comparando escalas a las frecuencias de afinación A=440 y A=432
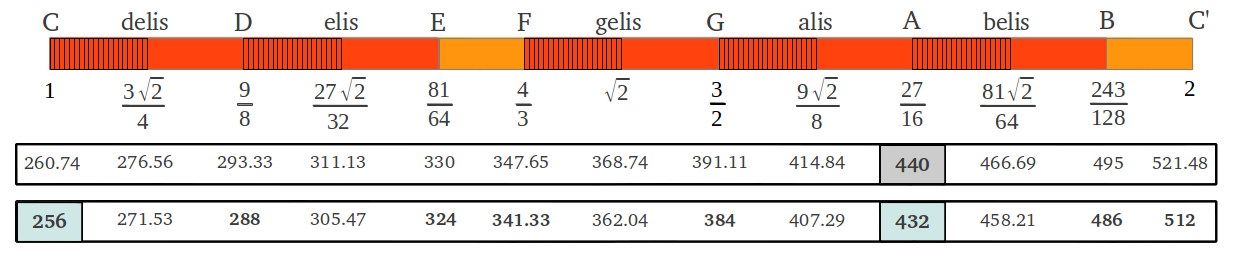
Las frecuencias de los tonos de la Escala del Temperamento Igual se muestran en la Figura 1 para diversos valores de la frecuencia de afinación. Aquí se puede apreciar claramente que la estructura de la escala -es decir la longitud de sus intervalos- se preserva, mientras que las frecuencias de los tonos individuales son distintas para cada método de entonación. Las frecuencias de los tonos a A=440Hz son muy distintas de las de A=432Hz. Afinando a C=256Hz (una octava por encima de la 'c=128Hz filosófica') proporciona frecuencias muy similares pero no iguales que afinando a A=432Hz en la Escala del Temperamento Igual. En cambio, esos dos métodos de afinación coinciden en la escala de Doce Quintas (Figura 1b) porque esta escala contiene los intervalos verdaderos de la escala diatónica griega de Aristógeno.
|
|
|
|
|
|
| Figura 1: Frecuencias de los tonos (en Hz) de (a) la Escala del Temperamento Igual y (b) la Escala de Doce Quintas para frecuencias de afinación A=440Hz, A=432Hz y c=128Hz. |
También resulta interesante darse cuenta de que, para un método de afinación determinado, la frecuencia de cualquier nota particular es muy parecida en la Escala del Temperamento Igual y en la Escla de Doce Quintas. Por lo tanto, si usted toca el piano pero no quiere cambiar a la escala de Maria Renold, puede probar la frecuencia de afinación A=432Hz tan sólo reafinando tu piano a esa frecuencia, sin que sea necesario cambiar de escala. Maria Renold explica el caso de "una señora que era cantante de ópera y enseñaba piano; hacía más de 20 años que había afinado su piano a C=256Hz y se había dado cuenta de que con esta frecuencia de afinación su talento vocal, que había perdido la elasticidad natural debido a la edad o a cantar de forma incorrecta, enseguida volvió a ser flexible y recuperó su frescor habitual". Según ella "afinar a c=128Hz posibilita al organismo humano balancear distintos tipos de disarmonías existentes de forma mejor y más rápida. Una voz educada de esta forma puede adaptarse fácilmente y dominar los problemas relacionados con el cantar en público y con la afinación tensa de hoy en día" [1, p.79].
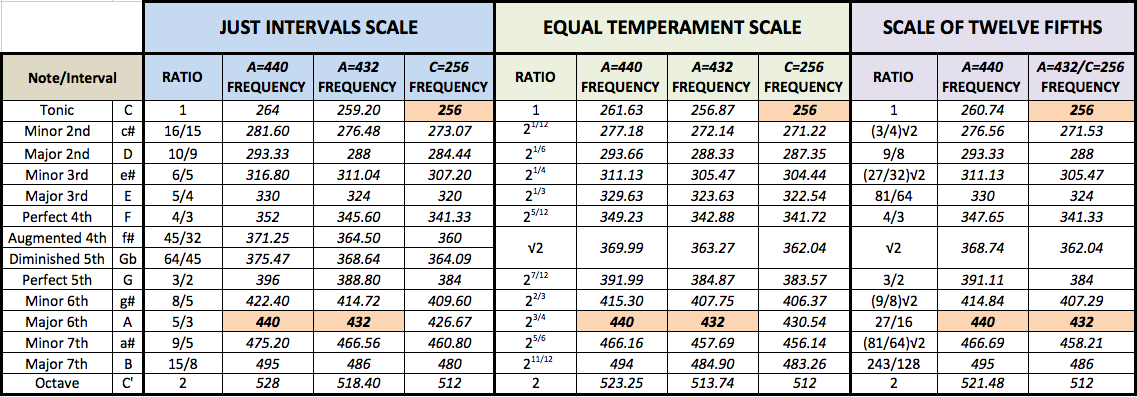
La Tabla 1 compara las frecuencias de los tonos individuales usando los tres métoos de afinación, en la dos escalas previas y también en la Escala de Intervalos Justos:
 |
|
| Table 1 |
3.- Experimentos con las frecuencias de tonos individuales
Maria Renold llevó a cabo experimentos muy sencillos, limitándose a dos pares de tonos basados en las frecuencias de afinación c=128Hz/A=432Hz y A=440Hz, y sus octavas. Las frecuencias de los dos pares de tonos fueron las siguientes [1, p.74]:
(1) c = 128.000 Hz y c = 130.813 Hz (ubicadas una octava por debajo de C = 256.000 Hz y C = 261.626 Hz, ver Tabla 1)
(2) a1=108.000 Hz y a1 = 110.000 Hz (ubicadas dos octavas por debajo de A = 432.000 Hz y A = 440.000 Hz, ver Tabla 1)
Los experimentos auditivos se llevaron a cabo con estos dos pares de tonos en más de 2000 personas de todas las edades y con distintas ocupaciones en EE.UU., Italia, Alemania y Suiza, y se registraron los resultados. Se hicieron esfuerzos para crear una atmósfera lo más natural y libre posible. A los participantes se les decía que la frecuencia de los tonos no era importante, sino que lo que interesaba era el carácter de cada uno de ellos. Los tonos se tocaban uno detrás de otro las veces necesarias, y la secuencia se iba variando. La pregunta cardinal era: ¿tienen los dos tonos de cada par un efecto distinto, aunque su diferencia de frecuencia sea mínima?
Citando a Maria Renold "los resultados fueron extraordinariamente interesantes e inequívocos. Prácticamente todos los participantes dijeron que para ellos como oyentes los dos pares de tonos y sus octavas tenían unas cualidades individuales inconfundiblemente distintas. No resultaba fácil poner esas cualidades en palabras puesto que se trataba de una experiencia nueva e inesperada [...] Durante el curso de los años se hicieron muchas comparaciones de este tipo, usando [el monocorde y], por ejemplo, flautas caseras de bambú, violines de estudiante e instrumentos de concierto, tocando los tonos con el instrumento mejor y después con el menos bueno. El resultado siempre era el mismo, cada tono demostraba tener una cualidad inherente y esa cualidad se mantenía constante, sin importar en qué registro o con qué instrumento se tocara. Por lo tanto podemos estipular que la cualidad individual de los tonos de origina en los propios tonos, y no en los instrumentos con los que se tocan" [1, p.74].
Después de haber establecido que los tonos elegidos tenían cualidades inherentes evidentes, se intentó, a pesar de las dificultades previsibles, averiguar de una forma más precisa cuales fueron las impresiones auditivas de los oyentes para cada par de tonos. A los participantes se les preguntó cuál de los dos tonos de cada par preferían. Sus respuestas fueron sorprendentes: "A pesar de que a1=110Hz (440Hz) era el tono más familiar, sólo el 3-8% de los participantes lo prefería; c = 130.828 Hz (261.656Hz) aún lo preferían menos personas. En otras palabras, alrededor del 90% de los oyentes prefería c = 128 Hz y a1 = 108 Hz (la octava inferior de A=432Hz)" [1, p.76].
Se preguntó a los oyentes cuál era la razón para sus preferencias. Se tocaron de nuevo los tonos tantas veces como fue necesario. Tal como ya hemos dicho, estos experimentos se llevaron a cabo durante 20 años y con muchas personas. A continuación se detalla un breve resumen de las respuestas obtenidas [1, p.76-77]:
|
Porcentaje |
a = 220 Hz (y a1 = 110 Hz) | a = 216 Hz (y a1 = 108 Hz) |
|---|---|---|
| 3-8% |
- sonaba bello |
- sonaba impersonal |
| sobre el 90% |
- sonaba desagradable |
- sonaba correcto y completo |
|
Porcentaje |
C = 261.565 Hz (y c = 130.828 Hz) | C = 256 Hz (y c = 128 Hz) |
|---|---|---|
| 3-8% |
- sonaba alegre |
- estimulaba preguntas - tenía un efecto inquietante |
| over 90% |
- sonaba mordaz |
- pertenecía al ser humano |
A continuación recogemos algunas respuestas más detalladas de profesores y músicos que habían desarrollado una actitud más consciente hacia la música [1, p.78]:
- "Independientemente los unos de los otros, un violinista y profesor de avanzada edad, un estudiante joven y un terapeuta se dieron cuenta de inmediato de que A = 432 Hz era el tono al cual ellos afinaban habitualmente sus instrumentos cuando tocaban por su cuenta.
- Una violista de concierto que hasta entonces había estado usando la frecuencia de afinación habitual, a menudo había notado al enseñar a adultos y niños que mucho de ellos tendían a sufrir nerviosismo y falta de concentración. Entonces afinó todos los instrumentos, incluyendo el suyo propio, a c = 128 Hz y A = 432 Hz. El resultado fue que gran parte del nerviosismo desapareció y que los estudiantes eran capaces de componer música con una mayor armonía.
- Un niño de dos años (aún ni músico ni profesor) que sabía andar pero aún no hablaba y que estaba presente en uno de los experimento auditivos, estaba pacíficamente sentado con un rostro feliz al lado de sus padres mientras se tocaban los tonos c = 128 Hz y C = 256 Hz, a1 = 108 Hz y a = 216 Hz. Cuando se tocaron los tonos a1 = 110 Hz y a = 220 Hz, y c = 130.813 Hz y C = 261.626 Hz, mostró un malestar evidente, poniéndose cada vez más y más inquieto, y finalmente protestando en contra de esos tonos pataleando fuertemente alrededor de la habitación.
- Dos profesoras sanadoras estaban familiarizadas con la frecuencia de afinación A = 440 Hz. Habiendo tomado parte en los experimentos y escuchado los tonos a1 = 108 Hz y a = 216 Hz, y c = 128 Hz y C = 256 Hz les resultó tan chocante la cualidad provocativa de a1 = 110 Hz y a = 220 Hz que decidieron a partir de entonces afinar sus instrumentos a c = 128 Hz".
Independientemente de Maria Renold, diversos músicos y profesores han hecho observaciones parecidas. Sus observaciones coinciden con las de ella y demuestran que proceden de los propios fenómenos, y no están causadas por una influencia consciente o inconsciente de esa autora. Además de la profesora de piano y cantante de ópera citada en la sección previa, está también el caso de una profesora sanadora inglesa. Ella practicaba mucho canto sin acompañamiento con alrededor de 400 niños y adolescentes, y se dió cuenta de que todos sus alumnos manejaban las melodías sin dificultad y volvían correctamente al tono inicial cuando éste era C = 256 Hz, y eso no sucedía en absoluto cuando el tono era A = 440 Hz [1, p.79].
Una opinión propia sobre las cualidades inherentes de los tonos individuales que se han descrito sólo se puede obtener escuchándolos y dejando que actúen sobre uno mismo, pero es muy importante que se toquen con un instrumento no eléctrico. Todos los experimentos que Maria Renold llevó a cabo con tonos producidos de forma electrónica fracasaron. Los tonos producidos incluso con los equipos de más alta calidad, sin importar a qué frecuencia, "tenían todos la misma cualidad sin excepción, y de hecho una cualidad de amplio vacío. Resultaría erróneo, no obstante, concluir de ello que los tonos electrónicos son más sencillos para los seres humanos porque eliminan la cualidad individual de cada tono. Al contrario, la electricidad impone su propia cualidad sobre los tonos, y eso es siempre así tanto si el sonido se produce de forma electrónica como si meramente se amplifica. Puede describirse de forma metafórica como un chirrido vacío" [1, p.73]. En un conjunto de experimentos en los que se grabaron y se reprodujeron mediante un equipo de alta calidad los tonos producidos con instrumentos reales, "se podía percibir una sombra de las cualidades de los tonos, pero no las propias cualidades en sí". Sin embargo, estas observaciones no deberían impedirnos experimentar con la música reproducida de forma electrónica a una nueva frecuencia de concierto A = 432 Hz o C = 256 Hz. Por ejemplo una buena amiga mía ha experimentado una gran mejora en las cualidades inherentes de diversas piezas musicales -especialmente ópera- que fueron originalmente producidas a A=440Hz, después de reconvertirlas a A = 432 Hz.
4.- Frecuencias de afinación para los Modos Aulós Griegos
En el artículo previo, hemos mostrado la rica estructura de intervalos de las siete escalas antiguas conocidas como Modos Aulós griegos, que eran las escalas musicales que se estudiaban en realidad en la escuela pitagórica. Sin embargo, no se mencionó nada acerca de la frecuencia de afinación de esas escalas. Según Maria Renold, "para permitir a los seres humanos modernos trabajar de forma segura con los modos, resulta necesario que, además de tener cuidado con la entonación de los intervalos, se preste atención también a la frecuencia de la tónica de cada escala individual. Los modos tienen un efecto muy poderoso y influyen en la organización física y rítmica del ser humano. Esto ya lo observó [su redescubridora] Kathleen Schlesinger" [1, p.85].
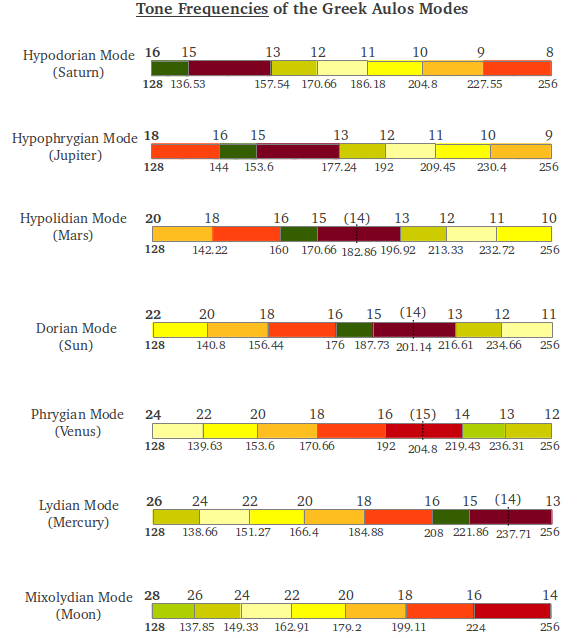
La Sta. Schlesinger afinaba los modos usando la frecuencia fundamental c = 128 Hz. Si estamos tocando los modos en un monocorde, esta es la frecuencia obtenida cuando se toca la longitud completa de la cuerda. Con esta restricción, existen aún dos formas de afinar los modos. La primera alternativa, la que usaba Schlesinger, consiste en dividir la longitud de la cuerda en un número distinto de segmentos para cada modo seleccionado: 22 segmentos para el modo del Sol, 24 para el modo de Venus, etc. (ver la Figura 36 del artículo previo). De esta forma, todos los modos comparten la misma frecuencia tónica (128 Hz) pero la frecuencia de referencia genérica o Arché, dada por la longitud del intervalo más pequeño, es distinta para cada modo (Figura 2). Por ejemplo, la frecuencia genérica del modo del Sol sería 128·22 = 2816 Hz y la frecuencia genérica del modo de Venus sería 128·24 = 3072 Hz.
 |
|
| Figura 2: Frecuencias de los tonos (en Hz) para afinar los Modos Aulós griegos ajustando la cuerda a una frecuencia fundamental c=128Hz y usando un número distinto de divisiones de la cuerda para cada modo. |
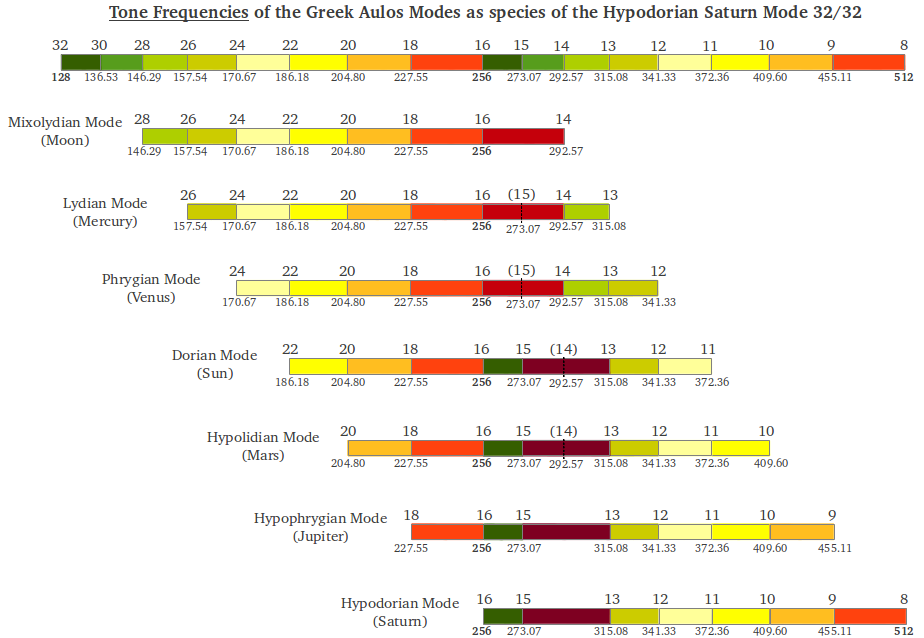
La otra alternativa para afinar los siete modos a partir de una fundamental de la cuerda c = 128 Hz es como subespecies de un modo común. Tal como se muestra en la Figura 3, si dividimos la longitud de la cuerda en 32 segmentos, la frecuencia genérica será 128·32 = 4096 Hz. Entonces cada modo se tocaría deslizándose a una octava distinta. Con este método, la frecuencia tónica es diferente para cada modo (186.18 Hz para el modo del Sol, 170.67 Hz para el modo de Venus, etc.) pero todos los modos comparten la misma mese (256 Hz).
 |
|
| Figura 3: Frecuencias de los tonos (en Hz) para afinar los Modos Aulós griegos como subespecies, ajustando la cuerda para una frecuencia fundamental c=128Hz y dividiendola en un número fijo de segmentos. Entonces cada modo se toca deslizándose a una octava distinta. |
Resulta muy informativo observar qué influencia tienen los dos métodos de afinación sobre la gente actual. Maria Renold reporta que años de observación han conducido a lo siguiente [1, p.85]: "Si se afinan los modos a la fundamental c = 128 Hz y mese = 176 Hz [en el modo del Sol, ver Figura 2] como hizo Schlesinger, se crea una especie de éxtasis entre los oyentes y un cierto grado de somnolencia tras una audición prolongada [...] En cambio no se observa ningún efecto sobre la mente de los oyentes de hoy en día con el modo del Sol afinado a una mese c = 128 Hz o C = 256 Hz y su fundamental a 186.182 Hz, eso es, con el tono genérico en c5 = 4096 Hz. Este método de afinación en realidad deja a los oyentes totalmente libres, permitiéndoles hacer arreglos musicales y configurar el modo de una forma completamente libre. Este segundo método de afinación [...] parece más adecuado para nuestra época".
Según la Figura 3, parecería que con este segundo método todos los modos deberían compartir las cualidades del modo de Saturno a partir del cual se han generado. Pero "al escuchar [el modo del Sol afinado de esta forma], uno se da cuenta de inmediato de que ese no es el caso, ya que se experimenta ese modo como una escala independiente y completamente válida. Es más, no sólo el modo del Sol sino también los otros seis modos planetarios suenan como modos originales, independientes con su tónica ubicada en distintos subtonos del tono genérico c5=4096 Hz [...] Por el contrario, si se tocan los modos con la tónica en los subtonos de otro modo planetario genérico de la fundamental común c = 128 Hz, por ejemplo en los del modo de la Luna 3328 Hz [28 segmentos en la cuerda, ver Figura 3], lo que sucede es que sólo el modo que pertenece al tono genérico [en este caso el modo de la Luna] suena auténtico y todos los demás modos suenan com especies o modos transpuestos. De ello se deduce que los subtonos del tono genérico c5=4096 Hz [...] son también los subtonos adecuados para los otros seis modos planetarios como escalas independientes. Una vez más se emplaza al lector a comprobarlo en el monocorde; con él, uno puede convencerse fácilmente de todo lo anteriormente expuesto". Si se desea afinar un instrumento según el método sugerido, la Tabla 15 en [1, p.88] explica cómo hacerlo paso a paso.
5.- Sobre las cualidades ocultas de un tono
¿Qué es un tono? Esta es una pregunta interesante, y tal vez está en la mente del lector después de todo lo que se ha discutido hatsa el momento. Yo clasificaría las características de un tono en cuantitativas y cualitativas. Las propiedades cuantitativas son aquellas objetivamente medibles. Las propiedades cualitativas tienen un efecto sobre nosotros como seres humanos, a pesar de que aun no sepamos cómo cuantificarlas. Por supuesto, la principal característica cuantitativa de un tono es su frecuencia: cuantas veces cicla por segundo. Sin embargo, cuando se produce un tono con un instrumento de cuerda -como el sencillo monocorde descrito en el artículo previo- no sólo se produce su frecuencia fundamental f~1/L. Una cuerda de longitud L puede vibrar, y de hecho vibra también a los múltiplos enteros de esta frecuencia. Esto es así porque su estructura fija permite la formación de ondas estacionarias con dos, tres y más nodos que "dividen" su longitud en dos (L/2), tres (L/3), y más fragmentos, produciendo sobretonos o armónicos a frecuencia 2f = 2/L, 3f=3/L, etc. (ver Figura 4).
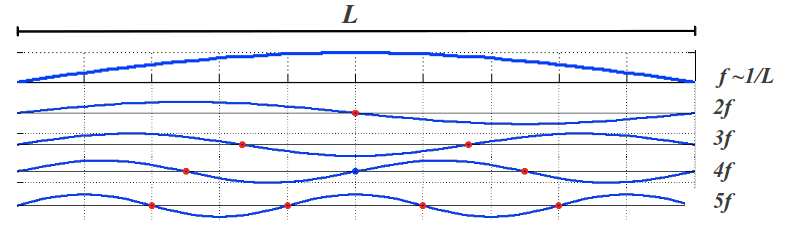 |
|
| Figura 4: Tocando una cuerda de longitud L se excita su frecuencia fundamental f así como sus armónicos 2f, 3f, ... |
A pesar de que los armónicos a menudo tinen mucha menor amplitud que la fundamental, el sonido total que se produce al excitar un tono en una cuerda contiene una mezcla de la fundamental de la cuerda y todos sus armónicos. Dependiendo de la forma exacta en que se toca la nota, los armónicos pueden tener amplitudes distintas. Como resultado, los músicos suelen decir que la nota tiene un timbre distinto. El principal cinstituyente del timbre proviene de la frecuencia fundamental y sus armónicos, aunque también se ve influenciado por componentes temporales del sonido como la envolvente temporal, el ataque, etc. [2]. Además, cuando una nota determinada se toca en instrumentos distintos, el tono resultante no tiene el mismo timbre, ya que cada instrumento produce armónicos de distintas amplitudes. La gente ha desarrollado escalas subjetivas de graduación para el timbre del tipo ligero/afilado, frío/templado, suave/duro, puro/rico, lleno/vacío, etc. Para una descripción más detallada del concepto de timbre véase la referencia [2].
Mi pregunta principal es: ¿puede el timbre de un tono estar detrás de las diferentes cualidades entre tonos distintos que han apreciado los oyentes de los experimentos de Maria Renold? Yo creo que no por la siguiente razón: las características cualitativas inherentes a un tono se mantenían en instrumentos distintos: la mayoría de la gente prefería a = 216 Hz por encima de a = 220 Hz independientemente del instrumento en el que se tocaran ambos tonos. Por lo tanto las cualidades inherentes a cada tono se preservan en los instrumentos distintos, pero sabemos por la discusión anterior que cambiando el instrumento también cambia el timbre de sus tonos. Luego el timbre no parece ser lo que causó que la gente prefiriese un tono en particular por encima de otro. Además, estas cualidades distintivas de un tono no estaban presentes cuando el tono se producía de forma electrónica.
Yo tengo la hipótesis de que las cualidades inherentes a un tono que se experimentan independientemente del instrumento pueden estar muy relacionadas con la interacción de la fuente del sonido con el espacio tridimensional. El llamado espacio vacío está muy probablemente estructurado. Buckminster Fuller ya consideró la posibilidad de que la estructura geométrica del espacio respondiera a su Matriz Isotrópica de Vectores (IVM): una red de tetraedros y octaedros interconectados con un Vector de Equilibrio en su centro. Esto es lo que yo he llamado la estructura interna del Cubo de Metatrón, una estructura que escala hacia dentro y hacia fuera, y cuyas coordenadas cartesianas pueden obtenerse exclusivamente a partir de números enteros y racionales, de hecho a partir de potencias de 2 y 3 como en la escala musical de Aristógeno. Para Fuller, la IVM es un marco conceptual que describe la simetría del espacio, con la cual los eventos energéticos pueden interactuar a través de su propiedad de jitterbug, produciendo una onda de actividad radiante [3, p.192]. Luego mi hipótesis es que, dependiendo de la frecuencia de la fuente de sonido, se produce un patrón de energía radiante distinto en el espacio (estructurado). Este patrón geométrico puede no ser capturado mediante micrófonos, pero interactuar con los cuerpos sutiles del ser humano, y puede ser la fuente de las cualidades inherentes del sonido que podemos percibir pero aún no somos capaces de cuantificar.
Existe tal vez una hipótesis más simple: el origen de las cualidades ocultas de un tono puede hallarse en la distribución tridimensional de energía sonora debida a la geometría de la sala. Diferentes frecuencias sonoras generan patrones de interferencia distintos. La distribución de sonido afecta no sólo a nuestros oidos, sino que puede percibirse en todo nuestro cuerpo. Esto podría explicar por qué esas propiedades geométricas del sonido prácticamente no se captan con uno o dos micrófonos. Por último, el verdadero mecanismo puede ser una combinación de ambos métodos, estando el espacio vacío (estructurado) activamente involucrado en la generación y transmisión de ese patrón geométrico asociado a una fuente de sonido.
6.- Referencias
[1] Renold, Maria: "Intervals, Scales, Tones and the Concert Pitch c = 128 Hz", Temple Lodge, 2004.
[2] Sethares, William A: "Tuning, Timbre, Spectrum, Scale", Springer, 2004.
[3] Edmondson, Amy C.: "A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller", EmergentWorld Press, 2007.