- Home
- Matemática Aurea
- Flor de la Vida
- Sólidos Sagrados
- Geometría sagrada y energía
- Y además...
- Modelos 3D
- Flor de la Vida 3D
- Sólidos Platónicos 3D
- Sólidos Arquimedianos 3D
- Sólidos de Catalan 3D
- Dodecaedro Disdiakis 3D
- Dodecaedro Pentakis 3D
- Dodecaedro Rómbico 3D
- Hexaedro Tetrakis 3D
- Hexecontaedro Deltoidal 3D
- Hexecontaedro Pentagonal 3D
- Icosaedro Triakis 3D
- Icositetraedro Pentagonal 3D
- Icositetraedro deltoidal 3D
- Octaedro triakis 3D
- Tetraedro Triakis 3D
- Triacontaedro Disdiakis 3D
- Triacontaedro Rómbico 3D
- Pirámides y Prismas 3D
- Estelaciones 3D
- Phi en ...
- Sólidos Sagrados en ...
- Música y geometría
- Acerca de
- Modelos 3D
Pirámides y Prismas
1.- Pirámides
Una pirámide es un poliedro formado conectando cada vértice de una base poligonal a un punto llamado ápex. Es un sólido cónico con base poligonal. Si no se especifica, habitualmente la base se supone que es cuadrada. Si la base es un polígono regular y el ápex está perpendicularmente encima de su centro, la pirámide es simétrica. El segmento que conecta el ápex con el punto medio de una arista de la base se llama apotema (Figura 1).
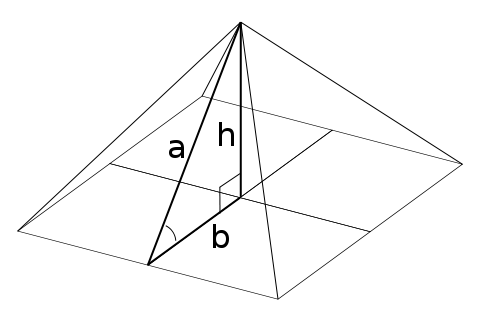 |
| Figura 1: Una pirámide cuadrangular genérica de base 2b, altura h y apotema a. |
Existen sólo tres pirámides cuya base es un polígono regular y cuyas aristas son todas iguales: el tetraedro, la pirámide cuadrangular y la pirámide pentagonal (Figura 2).
En general, dada una cara poligonal regular, la altura de la pirámidepuede tomar cualquier valor. Sin embargo, hay algunas pirámides cuadrangulares especiales, como la pirámide Aurea, en la cual el triángulo b:h:a de la Figura 1 es un triángulo de Kepler (sus lados obdecen a la progresión ); o la pirámide cuadrangular con una relación de altura a base h:b=4:π como la Gran Pirámide de Giza. Estas dos últimas pirámides aproximan muy bien la Cuadratura del Círculo.
Las pirámides con un polígono regular estrellado como base se conocen como pirámides estrelladas. Algunos ejemplos son las pirámides pentagrámica y heptagrámica mostradas en la Figura 3.
 |
 |
 |
| (a) Pentagrámica | (b) Heptagrámica I | (c) Heptagrámica II |
| Figura 2: Algunas pirámides estrelladas (haciendo click en la imagen se obtiene una vista 3D que se puede acercar, alejar y rotar). | ||
2.- Bipirámides y Prismas
Un poliedro cercano es la dipirámide (o bipirámide), que se forma uniendo dos pirámides base con base (Figura 3b). Esta operación esconde la "base" original que le da su nombre a la bipirámide. Las bipirámides són los poliedros duales de los prismas uniformes, que son prismas rectangulares con bases poligonales regulares y todas las aristas de igual longitud (Figura 3a). La figura siguiente muestra algunas bipirámides con sus correspondiente prisma dual:
|
PRISMA TRIANGULAR |
BIPIRÁMIDE TRIANGULAR |
|
CUBO |
OCTAEDRO |
|
PRISMA PENTAGONAL |
BIPIRÁMIDE PENTAGONAL |
|
PRISMA HEXAGONAL |
BIPIRÁMIDE HEXAGONAL |
|
PRISMA OCTAGONAL |
BIPIRÁMIDE OCTAGONAL |
|
PRISMA DECAGONAL |
BIPIRÁMIDE DECAGONAL |
| (a) Prismas uniformes | (b) Bipirámides |
| Figura 3: Haciendo click sobre cualquier imágen se obtiene una vista 3D que se puede acercar, alejar y rotar. | |
3.- Antiprismas y Deltoedros
Un antiprisma es un poliedro compuesto por dos copias paralelas de un polígono base conectadas por una banda alternada de triángulos (Figura 4a). Los antiprismas son similares a los prismas excepto que las bases están giradas la una en relación a la otra, y las caras laterales son triángulos en logar de cuadriláteros. Los antiprismas uniformes tienen triángulos equiláteros como caras laterales.
El poliedro dual de un antiprisma es un deltoedro (o trapezoedro o antibipirámide). Un deltoedro puede descomponerse en dos pirámides idénticas y un antiprisma central (Figura 4b). La figura siguiente muestra algunos antiprismas junto con su correspondiente deltoedro dual.
|
ANTIPRISMA CUADRANGULAR |
DELTOEDRO CUADRANGULAR |
|
ANTIPRISMA PENTAGONAL |
DELTOEDRO PENTAGONAL |
|
ANTIPRISMA HEXAGONAL |
DELTOEDRO HEXAGONAL |
|
ANTIPRISMA OCTAGONAL |
DELTOEDRO OCTAGONAL |
|
ANTIPRISMA DECAGONAL |
DELTOEDRO DECAGONAL |
| (a) Antiprismas | (b) Deltoedros |
| Figura 4: Haciendo click sobre cualquier imágen se obtiene una vista 3D que se puede acercar, alejar y rotar. | |